最大流问题
设一个赋权有向图D=(V, E),在V中指定一个发点vs和一个收点vt ,其它的点叫做中间点。对于D中的每一个弧(vi , vj)∈ E ,都有一个非负数 cij ,叫做弧的容量。我们把这样的图D叫做一个容量网络,简称网络,记做D=(V,E,C)。
流,即加在网络各条弧上的一组负载量。
例如:
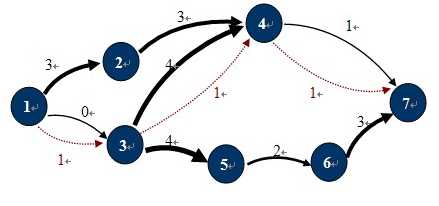
如图,在这个运输网络中,源点S和汇点T分别是1,7,各边的容量为C(u,v)。图中红色虚线所示就是一个可行流。
残余网络 增广路径 反向弧
 —————————>
—————————>
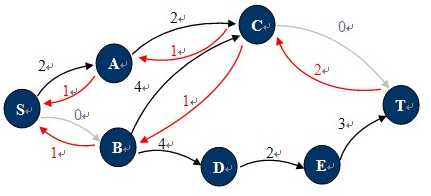
残余网络
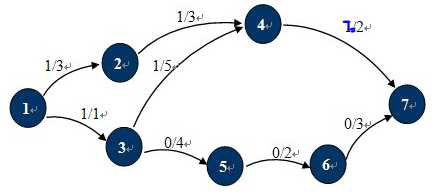
也许现在你已经知道什么是残余网络了,对于已经找到一条从S 到T的路径的网络中,只要在这条路径上,把 C(u,v) 的值更新为C(u,v) - P(u,v),并且添加反向弧 C(v,u)。对应的增广路径 Path 为残留网络上从S到T的一条简单路径。例如:原图中1,2,4,7就是一条增广路径,当然还有1,3,4,7。
此外在未做任何操作之前,原始的有向图也是一个残余网络,它仅仅是未做任何更新而已。
最大流定理:如果残留网络上找不到增广路径,则当前流为最大流;反之,如果当前流不为最大流,则一定有增广路径。
Ford-Fulkerson方法
用Ford-Fulkerson方法求最大流。为什么叫Ford-Fulkerson方法而不是算法,原因在于可以用多种方式实现这一方法,方式并不唯一。下面介绍一种基于广度优先搜索(BFS)来计算增广路径P的算法:Edmonds-Karp算法。
算法流程如下:
设队列Q:存储当前未访问的节点,队首节点出队后,成为已检查的标点;
Path数组:存储当前已访问过的节点的增广路径;
Flow数组:存储一次BFS遍历之后流的可改进量;
Repeat:
Path清空;
源点S进入Path和Q,Path[S]<-0,Flow[S]<-+∞;
While Q非空 and 汇点T未访问 do
Begin
队首顶点u出对;
For每一条从u出发的弧(u,v) do
If v未访问 and 弧(u,v) 的流量可改进;
Then Flow[v]<-min(Flow[u],c[u][v]) and v入队 and Path[v]<-u;
End while
If(汇点T已访问)
Then 从汇点T沿着Path构造残余网络;
Until
汇点T未被访问
应该举例
入门题:http://poj.org/problem?id=1273
Description
Input
Output
Sample Input
5 4 1 2 40 1 4 20 2 4 20 2 3 30 3 4 10
Sample Output
50
code:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61 |
#include <cstdio>#include <queue>#include <memory.h>const
int M = 210;const
int INF = 0x7fffffff;int E, V, map[M][M], flow[M], path[M], maxFlow;int start, end; // 源点和汇点 std::queue<int> qu;// BFS求出最短的增广路径 int
bfs(){ int
u , v; while(!qu.empty()) qu.pop(); memset(path, -1, sizeof(path)); path[start] = 0;flow[start] = INF; qu.push(start); while(!qu.empty()){ u = qu.front(); qu.pop(); if(u == end) break; for(v = 1; v <= V; ++v){ if(path[v] == -1 && map[u][v]){ qu.push(v); path[v] = u; flow[v] = flow[u] < map[u][v] ? flow[u] : map[u][v]; } } } if(path[end] == -1) return
-1; return
flow[V]; // 一次遍历之后的流量增量}void
edmonds_karp(){ int
step, pre, cur; while((step = bfs()) != -1){ maxFlow += step; cur = end; while(cur != start){ pre = path[cur]; map[pre][cur] -= step; // 更新正向边的实际容量 map[cur][pre] += step; // 添加反向边 cur = pre; } }}int
main(){ int
k, u, v, c; while(scanf("%d%d", &E, &V) != EOF){ memset(map, 0, sizeof(map)); for(k = 0; k < E; ++k){ scanf("%d%d%d", &u, &v, &c); map[u][v] += c; } start = 1, end = V; //设定:源点和汇点 maxFlow = 0; if(V == 1) printf("INF\n"); edmonds_karp(); printf("%d\n", maxFlow); } return
0;} |
原文:http://www.cnblogs.com/liyangguang1988/p/3660421.html