Problem Statement |
| |
The purpose of a roundabout is to control the flow of
traffic at a busy intersection. A roundabout has 4 entry
points: from the North, East, South and West; and 4 exit
points at the same locations (see Example 0 for a
diagram).
Cars can enter, leave or move one position on the
roundabout. Each of those events requires one second. All the
events can take place simultaneously. So if there are two cars
on the roundabout, one behind the other, then they can both
move during the next second. A car decides whether to enter
the roundabout based on its knowledge from the previous
second. A car will always enter if it has the right to do
so.
A car has the right to enter only if there are no cars to
its immediate left (either on the roundabout or waiting to get
on the roundabout) and it is the first car in line at the
entry point (Example 1 demonstrates this). A special case
occurs if there is a car at each of the 4 entry points. In
this case, the car from the North will wait until there are no
cars to its left on the roundabout and then will be the first
to enter.
Once the car is on the roundabout, it moves
counter-clockwise until it exits the roundabout. There are 4
positions on the roundabout. So for example, it would take 1
second to enter the roundabout, 2 seconds to complete half a
lap and another 1 second to exit the roundabout.
Each parameter of the input is a second by second account
of cars coming from that direction with their intended exit
locations. Intended exit locations will be N (North), E
(East), S (South) and W (West). A ‘-‘ means that no car
arrived during that second at the given entry point. Thus, for
example, character i of north
represents the direction in which a car (if there is one)
arriving from the north at time i will leave the
roundabout. So, at time i, this car will be added to
the end of the line at the north entry point to the
roundabout. Cars will not be allowed to exit the roundabout at
the point of their entry.
Given the lists of cars coming from the 4 directions,
return the total time required for all cars to leave the
roundabout. |
Definition |
| |
| Class: |
Roundabout |
| Method: |
clearUpTime |
| Parameters: |
String, String, String, String |
| Returns: |
int |
| Method signature: |
int clearUpTime(String north, String east, String
south, String west) |
| (be sure your method is public) |
|
Limits |
| |
| Time limit (s): |
2.000 |
| Memory limit (MB): |
64 | |
Constraints |
| - |
north, east,
south and west will contain
between 0 and 50 characters inclusive. |
| - |
north, east,
south and west must only
contain ‘N‘, ‘W‘, ‘S‘, ‘E‘ and ‘-‘ characters. |
| - |
north will NOT contain the character
‘N‘. |
| - |
east will NOT contain the character
‘E‘. |
| - |
south will NOT contain the character
‘S‘. |
| - |
west will NOT contain the character
‘W‘. |
Examples |
| 0) |
|
| |
|
|
Returns: 6 |
Note for plugin users: this
example contains an image. Please view the problem
in the applet to see the image.
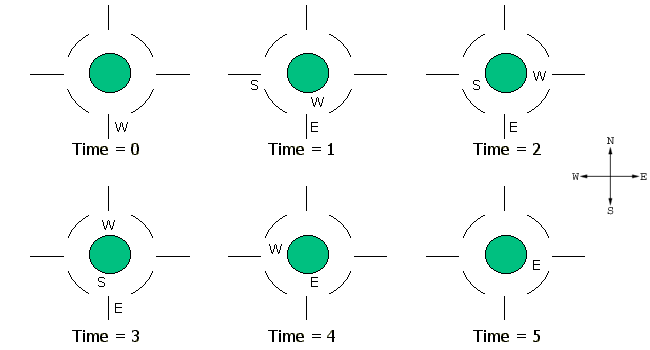
At
the start, a car approaches
the roundabout from the
South. At time = 1, the car going West enters the
roundabout, another car
approaches from the South and
another one from the West. At time = 2, the car
going West moves one
position, the car going East must give
way, the car going South enters the
roundabout. At time = 3, the
car going West moves one position, the car
going East must still give way, the
car going South moves one
position. At time = 4, the car going West
moves one position, the car going
South exits the roundabout,
the car going East enters the roundabout. At
time = 5, the car going West exits
the roundabout, the car
going East moves one position. At time = 6, the
car going East exits the
roundabout. The method should
return 6.
| | |
| 1) |
|
| |
|
|
Returns: 9 |
| All the cars from the North must
wait until the cars from the East exit the
roundabout. Only then can they enter the
roundabout. | |
|
| 2) |
|
| |
"SSS" |
"WW-" |
"N" |
"S------" | |
Returns: 13 |
| | |
| 3) |
|
| |
"SSS-" |
"--W---W" |
"WE" |
"-S" | |
Returns: 14 |
| | |
| 4) |
|
| |
|
| 5) |
|
| |
|
| 6) |
|
| |
|
|
Returns: 6 |
| Note: At time = 3, the car from
the South does not enter the roundabout, because
it has already decided not to enter, based on its
knowledge from the previous second. Thus it enters
at time = 4. | |
|
| 7) |
|
| |
|
| 8) |
|
| |
|