算法分析与设计复习

2016年初，研一上学期期末考试前，复习并总结算法分析与设计科目的内容。复习过程参照《算法导论》中文第2版，同时参照PPT，章节划分根据PPT内容

概要：

第一章 概述

第二章 插入排序&分治策略

第三章 复杂度分析

第四章 堆与堆排序

第五章 快速排序

第六章 线性时间排序

第一章 概述

1. 算法的应用范围

   算法在诸如生物等诸多领域有其应用

2. 算法的意义

   算法在很多情况下让不可能完成的事情变成了可能，让处理的很慢的过程变快。

3. 一个铺垫

   一串不全为0的数，怎么取能拿到一段和最大的子串

第二章 插入排序&分治策略

1. 插入排序

   • 掌握插入排序的方法

   • 循环不变式的证明（不考）

     初始化：

     保持：

     终止：

   • 逐步计算插入排序的时间复杂度：

     结论(基于RAM模型下)：

     Best Case：O（n）

     Worst Case：O（n^2）

2. 分治策略

   • 概述：

     大问题拆成多个小问题，分别计算每个小问题的解最后把多个小问题合成原问题的解

3. MERGE Sort

   • 掌握归并排序的方法

   • 分析归并排序

     • Best case:nlgn
     • Worst case:nlgn

4. 课后习题总结

   • 推演一个插入排序的过程
   • 循环不变式证明线性查找的正确性
   • 对给定的时间复杂度表达式写出Θ
   • 推演一个MERGE Sort
   • 算法设计题：可以看＊

第三章 复杂度分析

1. 时间复杂度分析

   • O（n）¹上界

     • o不精确的上界

   • Ω（n）²下界

     • ω不精确的下界
   • θ（n）³精确界

2. 归并排序分析

   • 代换法

     • 做一个好的猜测
     • 假设这个界对某一个范围内成立
     • 带入得出结论
     • 数学归纳法证明结论正确

   • 递归树

     • 时间复杂度的表达式是每一层拆分开销之和加上最底层每一个未知的开销。

   • 主定理

     • 形如：T（n）＝aT（n／b）＋f（n）

     • 三种情况：

       • 若存在ε>0，有f(n)=O(n^(log b(a)-ε)),则T(n)＝Θ(n^(log b(a)))
       • 若f(n)=Θ(n^(log b(a))),T(n)=Θ(n^(log b(a))lg(n))
       • 若对某ε>0,有f(n)=Ω(n^(log b(a)+ ε)),且对常数c<1与所有足够大的n，有af(n/b)<=cf(n),则T(n)=Θ(f(n))

3. 课后习题总结

   • 代换法证明时间复杂度

     • 猜测渐进确界，证明之
     • 主方法可用情况的练习
     • 判断主方法是否可用，确定渐进上界

第四章 堆与堆排序

1. 堆的概念

   • 利用树的数组存储方式，PARENT(i) = ?, LEFT(i) = 2i, RIGHT(i) = 2i + 1

2. 两个关键的函数

   • MAX-HEAPIFY 已有堆的情况下，加入新结点后调整堆以使得其满足堆的条件。O(lgn)
   • BUILD-MAX-HEAP 基于无序数组调整为大顶堆Θ(n)
   • 其中，BUILD-MAX-HEAP是由(n/2)向下取整次MAX-HEAPIFY组成的，但其时间复杂度是Θ(n)

3. 堆排序时间复杂度

   • 时间复杂度由两部分组成，1次BUILD-MAX-HEAP，n-1次MAX-HEAPIFY，故结果为T(n)=Θ(n)+nO(lg n)=O(nlgn)
   • 最好的情况下，时间复杂度为O(n)
4. 优先级队列

5. 必会技能：

   • 区分一个数组是不是堆
   • 手工跑堆排序或者建堆过程

6. 课后习题总结：

   • 区分一个序列是否为最大堆
   • 画出一个完整的MAX-HEAPIFY流程

第五章 快速排序

1. 快速排序

   • 时间复杂度

     • 最好Θ(nlgn)
     • 平均Θ(nlgn)
     • 最坏Θ(n2)
   • 知道分治的过程————以一个数做分治，分成两组
   • 掌握快排的手动做法
   • 有一个关于每次都从1/10位置分隔的情况下仍为nlgn的证明

2. 随机快排

   • 关键：用随机来避免出现Worst case
   • 实际表现是最快的排序

   • 时间复杂度

     • 平均Θ(nlgn)
     • 最坏Θ(n2) （仅在理论上存在）

3. 课后习题总结

   • 若快排数组中元素都一样，时间复杂度是多少？
   • 答：这是Worst Case 所以是Θ(n2)

第六章 线性时间排序

1. BDD证明比较类排序最坏情况的下界是nlgn

2. 计数排序

   • 计数排序是一种稳定排序
   • 时间复杂度Θ(k+n) ，在k与n同一数量级时，该复杂度为O(n)

   • 关键：被排序的n个数在0～k之间

     • 若这n个数的范围是n^2，则时间复杂度不再是O(n),而是O(n^2)

   • 掌握计数排序的完整过程，可以手跑

     1. 创建一个容量为k的数组C，并将所有元素置零
     2. 遍历原数组A，在C中对应的位置+1
     3. 遍历数组C，从第2个元素开始的所有元素的值依次用前一个元素与当前元素的和替换。
     4. 逆序遍历A，拿到元素a，在C中查找其位置（即C中元素对应的数值）在数组B中的对应位置放入a即可。同时将C中的那个数据-1

3. 基数排序

   • 掌握基数排序的完整过程，可以手跑
   • 基数排序的特点：利用稳定排序的特点，从低位到高位按位排序

   • 时间复杂度

     • Θ(d T(n))
     • 在每位计算使用计数排序的时候，时间复杂度为Θ(n)

4. 桶排序

   • 掌握桶排序的完整过程，可以手跑
   • 要点：类似于计数排序，为待排序数组提供若干个区间，将各个待排序的数放进区间内，完成区间内排序的同时，就得到了一个完整的排序结果。

5. 算法小结（重要考点）

   

1. 助记：O，my god——上帝、上界 ??
2. 助记：欧米伽——家在地上，下界 ??
3. 助记：θ的中间的一横足以说明是中间的啊～ ??

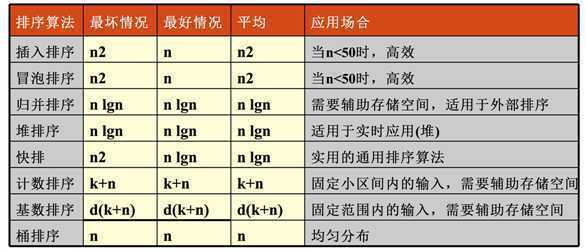
算法分析与设计复习

原文：http://www.cnblogs.com/jhalan6/p/5117405.html