要进行控制系统的仿真那么传递函数肯定少不了，那么它有几种常见的形式以及如何利用matlab创建呢？
如何构建呢？嘿嘿，如下：
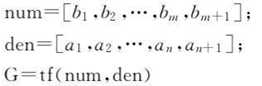
例如 ：
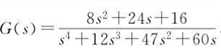
代码：
num=[8 24 16];
den=[1 12 47 60 0];
G0=tf(num,den)
结果：
对于离散系统同样适用，只不过增加了采样周期，
例如：
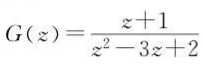采样周期为0.5s。
代码：
num=[1 1];
den=[1 -3 2];
Gz=tf(num,den,‘Ts‘,0.5)
具体语句格式：
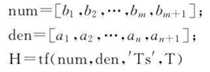
结果如下：
大家都知道这种形式的标准公式为：
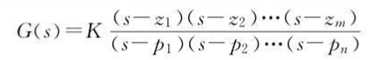
离散情况：
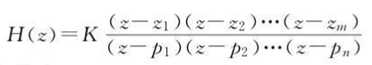
我们从他可以看出三个东西：1，零点z；2，极点p；3，增益K；
构造格式如下：（大家当然也可以把他展开，用tf构建）
例如：
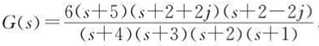
代码：
z=[-5 -2-2j -2+2j];
p=[-4 -3 -2 -1];
K=6;
G=zpk(z,p,K)
结果如下：
离散的情况就不用说了。
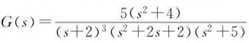
第一种方法：（具有通用性）
首先需要指明函数中的‘s‘，然后就可以构造符号函数了。
代码如下：
s=tf(‘s‘);
G=5*(s^2+4)/((s+2)^3*(s^2+2*s+2)*(s^2+5))
第一句指明用s代替tf函数中的‘s‘，
结果如下：
对于离散系统同样适用，只不过s变成了z并加上采样时间而已。
例如对于上面离散的例子：
z=tf(‘z‘,0.5);
H=(z+1)/(z^2-3*z+2)
结果：
第二种形式：（利用conv（）函数，当然也具有通用性，矩阵乘法）
由于我们将多项式表示为一维矩阵的形式，故多项式的运算当然可以用矩阵的相关运算来代替了（matlab不是称为矩阵实验室吗）。
C = conv(A, B) convolves vectors A and B.
格式如下：
对于
代码：
结果就不贴了。
所用函数为函数c2d(sysc,Ts,‘method‘);
sysc-所需要离散的连续传递函数
Ts-采样周期
Method-离散化方法，常用有以下几种：
例如：
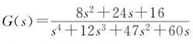采样周期为1s。
代码：
num=[8 24 16];
den=[1 12 47 60 0];
G=tf(num,den);
Ts=1;
G1=c2d(G,Ts,‘zoh‘)
G2=c2d(G,Ts,‘tustin‘)
结果如下：
调用函数为 d2c(sysd,‘method‘); method与c2d()函数一样,在这里就不啰嗦了。
现在已经知道了传递函数的构建与离散，还需要构造闭环传函，函数为feedback(Gs,Hs); 简单吧！
单位阶跃响应：step(sysc);
单位冲击响应：impulse(sysc);
其他。。。。。。
任意函数：lsim();
调用格式：
例如开环传函如下，求单位负反馈时单位阶跃响应：
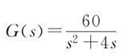
代码：
clear;
num=60;
den=[1 4 0];
Gs=tf(num,den);
close_Gs=feedback(Gs,1);
step(close_Gs)
结果如下：
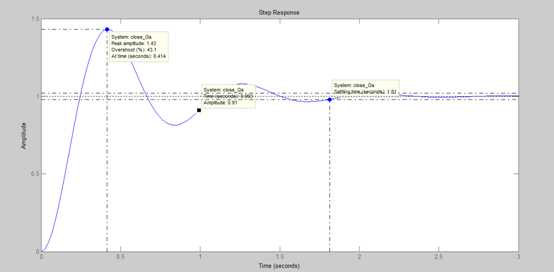
关于图像，直接在图像上右键，便可以看到系统的相关性能参数，比如超调量，上升时间，调整时间等。
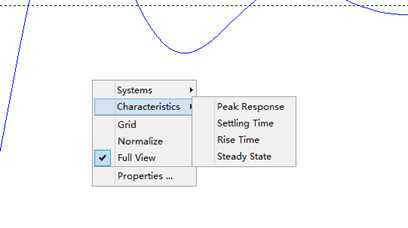
零极点分布图：pzmap(传递函数)；根轨迹分布图：rlocus(传递函数)；
例如：（只举例零极点分布图）
sys=tf([3 2 5 4
6],[1 3 4 2 7 2]);
pzmap(sys)
grid on
得到：叉符号代表极点，圆圈符号是零点，我们可以非常清楚的看到，这个系统具有右半平面的极点，所以这个系统是不稳定的！
与连续系统相同。
matlab提供了函数bode(),来绘制bode图；函数margin(),来求解幅值稳定裕度与相位稳定裕度。
格式：
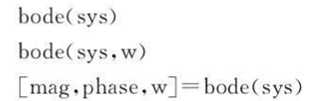
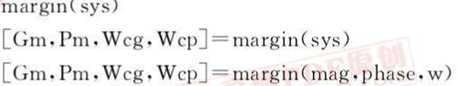
例如：传递函数
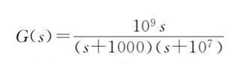
num=[10^9 0];
den=conv([1 1000],[1 10^7]);
sys=tf(num,den);
bode(sys);
grid;
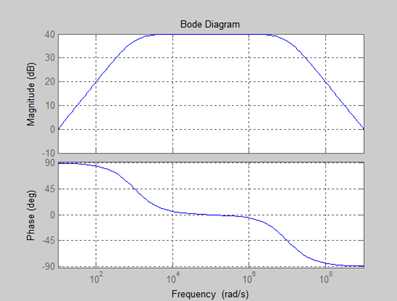
结果：
格式：
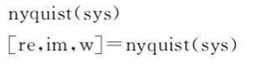
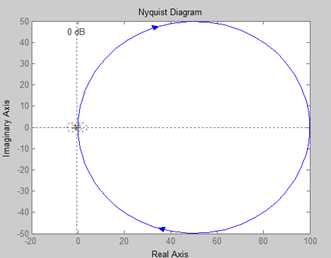
例如：
num=[10^9 0];
den=conv([1 1000],[1 10^7]);
sys=tf(num,den);
%bode(sys);
nyquist(sys);
grid;
结果：
原文：http://www.cnblogs.com/NeiHe/p/3663309.html