MATLAB 损失函数画图

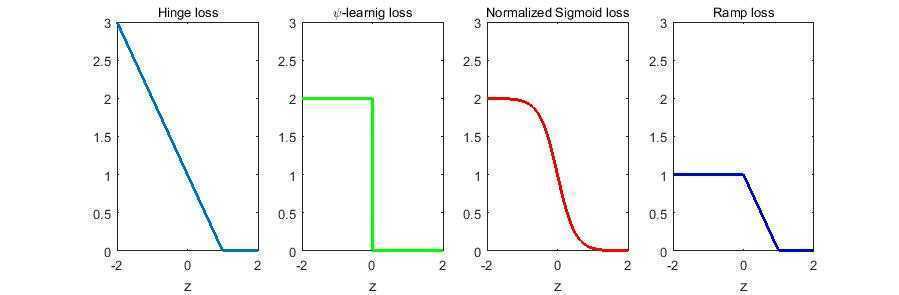
%plot loss function

%define the loss function
H = @(z)max(0,1-z) ; %Hinge loss function
P = @(z)(2*(z<0)+0*(z>=0)); %\psi-learning loss function
S = @(z)(1-tanh(2*z)); %Normalized Sigmoid loss function
R = @(z)(1*(z<0)+(1-z).*(z>=0&z<1)+0*(z>=1)); % ramp loss

z=-2:0.01:2;
subplot(1,4,1) % plot the 1st figure of 1-4
plot(z,H(z),‘-‘,‘linewidth‘,2);
xlabel(‘z‘);
title(‘Hinge loss‘,‘fontweight‘,‘normal‘,‘fontsize‘,10);
axis([-2,2 0 3])

subplot(1,4,2)
plot(z,P(z),‘g-‘,‘linewidth‘,2);
xlabel(‘z‘);
title(‘\psi-learnig loss‘,‘fontweight‘,‘normal‘,‘fontsize‘,10);
axis([-2,2 0 3])

subplot(1,4,3)
plot(z,S(z),‘r-‘,‘linewidth‘,2);
xlabel(‘z‘);
title(‘Normalized Sigmoid loss‘,‘fontweight‘,‘normal‘,‘fontsize‘,10);
axis([-2,2 0 3])

subplot(1,4,4)
plot(z,R(z),‘b-‘,‘linewidth‘,2);
xlabel(‘z‘);
title(‘Ramp loss‘,‘fontweight‘,‘normal‘,‘fontsize‘,10);
axis([-2,2 0 3])