所谓图元的生成,是指完成图元的参数表示形式(由图形软件包的使用者指定)到点阵表示形式(光栅显示系统刷新时所需的表示形式)的转换。通常也称扫描转换图元。
直线的扫描转换:确定最佳逼近于该直线的一组像素,并且按扫描线顺序对这些像素进行写操作。
三个常用算法:1、数值微分法DDA;2、中点画线法;3、Bresenham算法。
生成目标,求与直线段充分接近的像素集
生成前提条件:1、像素网格均匀,坐标为整数值;2、直线段的宽度为1;3、直线段的斜率k的取值范围为[-1,1]。
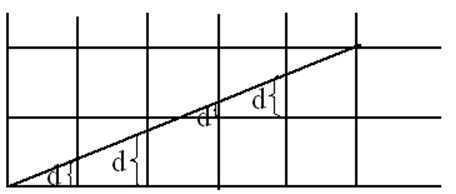
已知过端点P0 (x0, y0), P1(x1, y1)的直线段L: y=kx+b 直线斜率为 k = (y1 - y0)/(x1 - x0),x从左端点x0开始,向右端点x1以步长=1(个象素),计算相应的y坐标y=kx+b;取象素点(x, y(x))作为当前点的坐标。
计算yi+1 = kxi+1+b
= k1xi+b+kDx
= yi+kDx 其中Dx =1; yi+1 = yi+k 。
对应关系如下图所示:
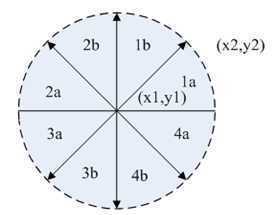
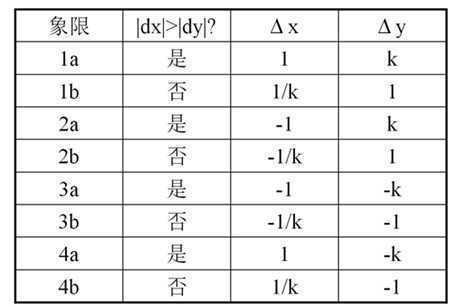
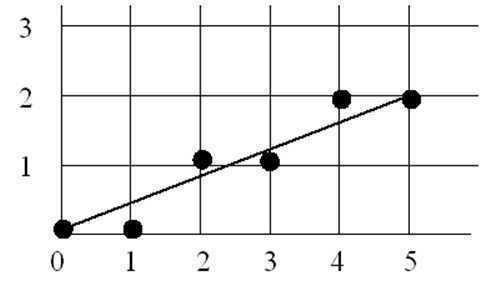
当前像素点为p(xp, yp) ,下一个象素点为P1或P2。设M=(xp+1, yp+0.5),为p1与p2的中点,Q为理想直线与x=xp+1垂线的交点。将Q与M的y坐标进行比较。
如下图所示:
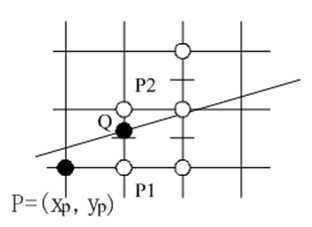
当M在Q的下方,则P2应为下一个象素点;
当M在Q的上方,应取P1为下一点。
构造判别式:d=F(M)=F(xp+1,yp+0.5) = a(xp+1)+b(yp+0.5)+c
其中a=y0-y1, b=x1-x0, c=x0y1-x1y0
当d<0,M在L(Q点)下方,取右上上方PU为下一个像素;
当d>0,M在L(Q点)上方,取右方PD为下一个像素;
当d=0,选P1或P2均可,约定取PD为下一个像素;
d是xp, yp的线性函数,因此可采用增量计算,提高运算效率。初值d0=F(x0+1, y0+0.5)=a+0.5b。
(1) 若当前象素处于d>=0情况,则取正右方像素PD(xp+1, yp), 要判下一个像素位置,应计算:di+1=F(xp+2, yp+0.5)=a(xp+2)+b(yp+0.5)=d+a; 增量为a。
(2) 若d<0时,则取右上方像素PU(xp+1, yp+1)。要判断再下一像素,则要计算:di+1= F(xp+2, yp+1.5)=a(xp+2)+b(yp+1.5)+c=d+a+b ;增量为a+b。
画线从(x0, y0)开始,d的初值d0=F(x0+1, y0+0.5)=F(x0, y0)+a+0.5b =a+0.5b。
可以用2d代替d来摆脱小数,提高效率。
用中点画线法画出P0(0,0) ,P1(5,2)的直线。
首先构造出判别式:d = a(xp+1)+b(yp+0.5)+c 。其中a = y0 - y1 = -2,b = x1 - x0 = 5,c = x0y1 - x1y0 = 0。
则初值d0 = a + 0.5b = 0.5。取点P‘(1,0)为下一个像素的位置。按照规则(1)、(2)计算,可以得到下列结果表:
|
i |
xi |
yi |
d |
|
1 |
0 |
0 |
0.5 |
|
2 |
1 |
0 |
-1.5 |
|
3 |
2 |
1 |
1.5 |
|
4 |
3 |
1 |
-0.5 |
|
5 |
4 |
2 |
2.5 |
用坐标表示,下图:
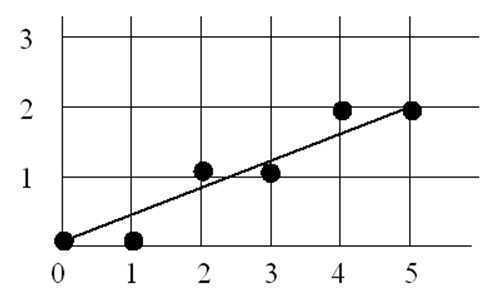
过各行各列象素中心构造一组虚拟网格线。按直线从起点到终点的顺序计算直线与各垂直网格线的交点,然后根据误差项的符号确定该列象素中与此交点最近的象素。
设直线方程为: 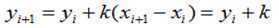 ,其中k=dy/dx。 因为直线的起始点在象素中心,所以误差项d的初值d0=0。
,其中k=dy/dx。 因为直线的起始点在象素中心,所以误差项d的初值d0=0。
x下标每增加1,d的值相应递增直线的斜率值k,即d=d+k。一旦d≥1,就把它减去1,这样保证d在0、1之间。
当d≥0.5时,最接近于当前象素的右上方象素(xi+1,yi+1)
当d<0.5时,更接近于右方象素(xi+1,yi)。
为方便计算,令e=d-0.5,e的初值为-0.5,增量为k。
当e≥0时,取当前象素(xi,yi)的右上方象素(xi+1,yi+1);
当e<0时,更接近于右方象素(xi+1,yi)。
用Bresenham算法画出P0(0,0) ,P1(5,2)的直线。
计算得出斜率k = dy/dx = 0.4。
结果如下表:
|
i |
x |
y |
e |
|
1 |
0 |
0 |
-0.5 |
|
2 |
1 |
0 |
-0.1 |
|
3 |
2 |
1 |
0.3 |
|
4 |
3 |
1 |
-0.3 |
|
5 |
4 |
2 |
0.1 |
|
6 |
5 |
2 |
-0.5 |
坐标表示:
上述Bresenham算法在计算直线斜率与误差项时用到小数与除法。可以改用整数以避免除法。由于算法中只用到误差项的符号,因此可作如下替换
这样e’的初值是-dx,由于k=dy/dx,所以e’的增量就变为2*dy。
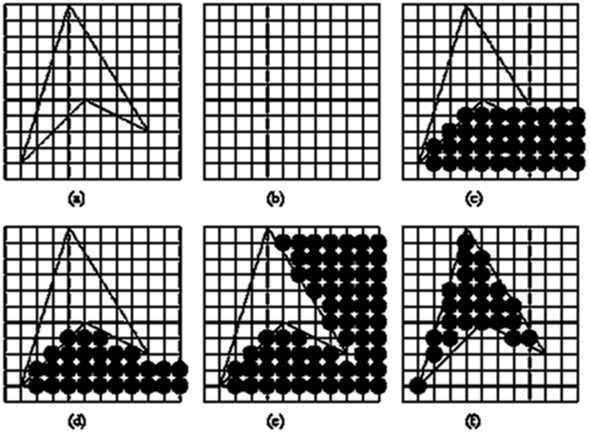
圆的特征:八对称性,只要扫描转换八分之一圆弧,就可以求出整个圆弧的像素集。
考虑中点在原点,半径为R的第二个八分圆,构造判别式(圆方程):
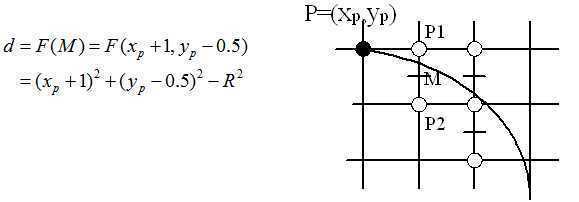
若d<0,则取p1为下一像素,并且下一像素的判别式为:
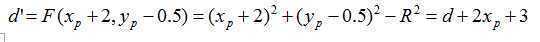
若d>=0,则取p2为下一像素,并且下一像素的判别式为:
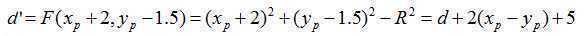
第一个像素是(0,R),判别式d的初始值为: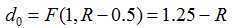
为了进一步提高算法的效率,可以将上面的算法中的浮点数改写成整数,将乘法运算改成加法运算,即仅用整数实现中点画圆法。使用e=d-0.25代替de0=1-R。
多边形有两种重要的表示方法:顶点表示法和点阵表示法。
多边形的扫描转换:把多边形的顶点表示转换为点阵表示。
共有4种方法:逐点判断法、扫描线法、边缘填充法、种子填充法。
逐个判断绘图窗口被的像素是否在多边形内。
判断点是否在多边形内部的方法:射线法,累计角度法。
从待判断点v发出射线,求交点个数k,k的奇偶性决定了点与多边形的内外关系:
若k为基数,则点在多边形内。
若k为偶数,则点在多边形外。
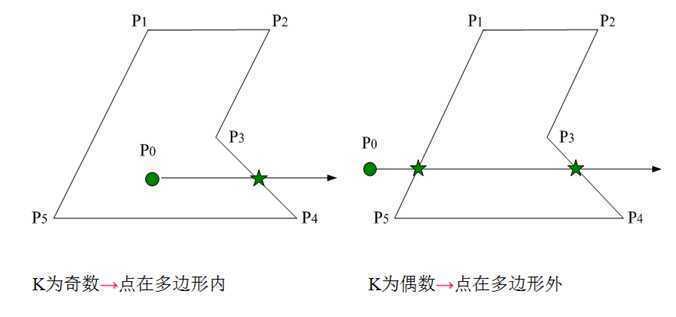
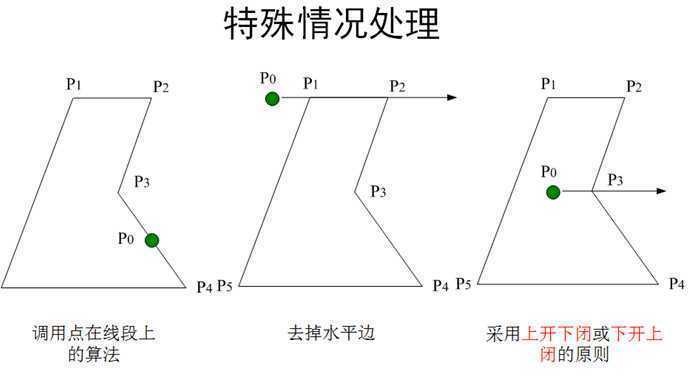
从v点向多边形p顶点发出射线,形成有向角 ![]() 。
。
计算有向角的和,得出结论:
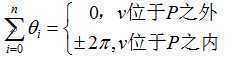
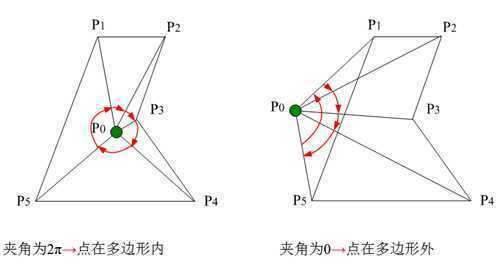
利用一条扫描线上的像素存在着连贯性这一特征(区域连贯性、扫描线连贯性和多边形边的连贯性)。避免对像素逐点判断和反复求交的运算。
1)区域连贯性:对于相邻的两个区域必有一区域是在多边形内部,另一个区域在多边形外部。
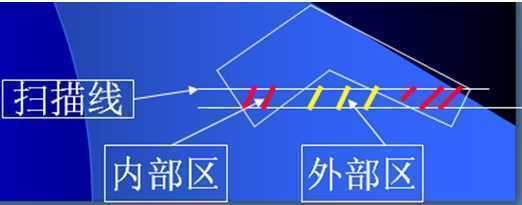
2)扫描线的连贯性:若扫描线y=j与多边形p相交,则交点数是偶数。且在扫描线上,只有区段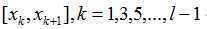 位于多边形p内。
位于多边形p内。
3)边的连贯性:若多边形p的边与扫描线y=k1至y=k2都相交,则边有下面关系:xi+1 = xi + 1/m。其中m=(Y2-Y1)/(X2-X1) 为多边形边的线段的斜率。
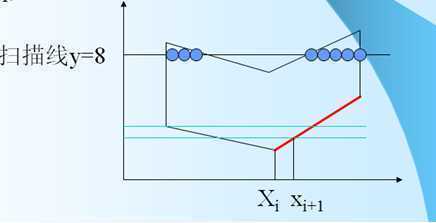
扫描线(Y-X)算法中扫描线要和所有的边求交,效率较低。因为一条扫描线往往只和少数几条边相交。
利用两个连贯性:
1.边的连贯性:当某条边与当前扫描线相交时,它很可能也与下一条扫描线相交。
当前扫描线与多边形某一条边的交点的x坐标为x,则下一扫描线与该边的交点不要重计算,只要加一个增量△x。
设该边的直线方程为:ax+by+c=0,若y=yi,x=x i;则当y = y i+1时,其中△x = -b/a为常数。
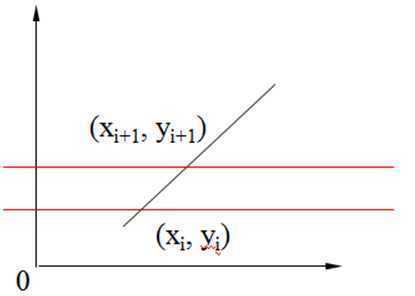
2.扫描线的连贯性:当前扫描线与各边的交点顺序,与下一条扫描线与各边的交点顺序很可能相同或类似。
Y-X算法的主要思想:
1、与当前扫描线相交的边称为活动边(active edge),把它们按与扫描线交点x坐标递增的顺序存入一个链表中,称为活动边表(AET, Active edge table)。
2、只需对当前扫描线的活动边表作更新,即可得到下一条扫描线的活动边表。
活性边表(AET):把与当前扫描线相交的边称为活性边,并把它们按与扫描线交点x坐标递增的顺序存放在一个链表中。
结点内容:
x:当前扫描线与边的交点坐标
△x:从当前扫描线到下一条扫描线间x的增量
ymax:该边所交的最高扫描线号ymax

边表桶(NET): 存放在该扫描线第一次出现的边。若某边的较低端点为ymin,则该边就放在扫描线ymin的新边表中。
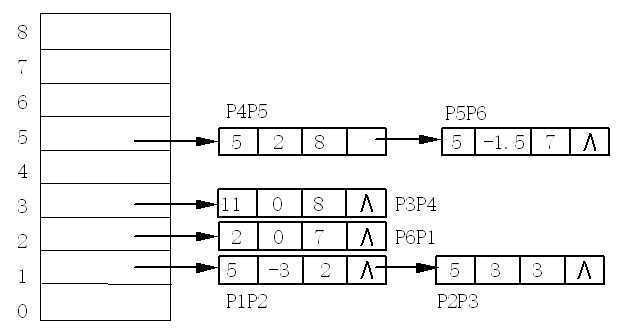
求余运算:假定A为一个正整数,则M的余定义为A – M, 记为  。计算机中取A为n位能表示的最大整数。即,A=0xFFFFFFFF。
。计算机中取A为n位能表示的最大整数。即,A=0xFFFFFFFF。
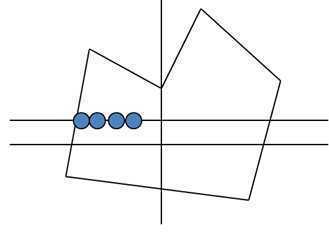
对于每条扫描线和每条多边形边的交点,将该扫描线上交点右方的所有像素取余。
① 将绘图窗口的背景色置为  ;
;
② 对多边形的每一条非水平边,从该边上的每个象素开始向右求余;
基本思想:
帧缓冲器中对多边形的每条边进行直线扫描转换,即对多边形边界所经过的象素打上标志,然后再采用和扫描线算法类似的方法将位于多边形内的各个区段着上所需颜色。使用一个布尔量inside来指示当前点是否在多边形内的状态。
1.区域的定义:
1)内定义区域:区域内部具同一种颜色,外部有一种颜色。
2)边界定义区域:边界具有一种特定颜色,边界内具有不是新值(填充色)。
3)四连通区域:各像素在水平和垂直四个方向是连通的。
4)八连通区域:各像素在八个方向是连通的。

区域填充指先将区域的一点赋予指定的颜色,然后将该颜色扩展到整个区域的过程。区域填充算法要求区域是连通的 。
用离散量表示连续量引起的失真现象称之为走样(aliasing),光栅图形走样的现象有:
n 阶梯状边界
n 图形细节失真(图形中的那些比像素窄的细节变宽)
n 狭小图形遗失和动态图形的闪烁
用于减少或消除这种效果的技术成为反走样(antialiasing)
把显示器分辨率提高一倍:直线经过两倍的像素,锯齿也增加了一倍,但同时每个阶梯的宽度也减小了一倍。所以显示出的直线段看起来就平滑了一些。
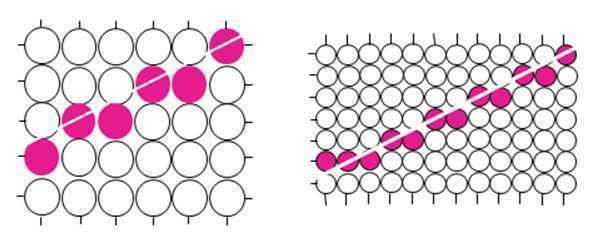
优缺点:增加了分辨率虽然简单,但不是一种经济的方法;显示器的水平、竖直分辨率各提高一倍,则显示器的点距就减少一倍,帧缓存容量则增加到原来的四倍,而扫描转换同样大小的图元却要花4倍的时间。而且它只能减轻而不能消除锯齿现象。
两个假设:
1.像素是数学上抽象的点,它的面积为0,它的亮度由覆盖该点的图形的亮度所决定;
2.直线段是数学上抽象直线段,它的宽度为0。
但是现实中的像素面积不为0,直线段的宽度至少为一个像素。假设与现实的矛盾是导致走向现象出现的原因之一。
每个象素是一个具有一定面积的小区域,将直线段看作具有一定宽度的狭长矩形。当直线段与象素有交时,求出两者相交区域的面积,然后根据相交区域面积的大小确定该象素的亮度值。
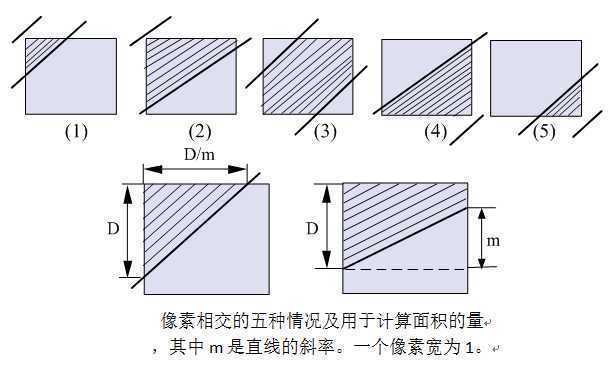
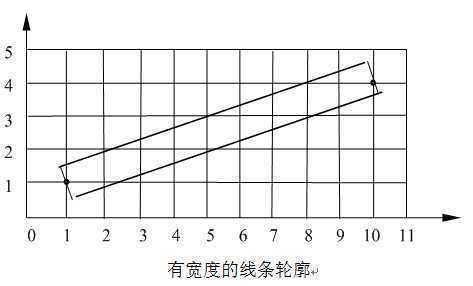
为了简化计算可以采用离散的方法:n=9,k=3近似面积为1/3
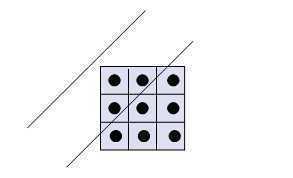
首先将屏幕象素均分成n个子象素 ,然后计算中心点落在直线段内的子象素的个数k,将屏幕该象素的亮度置为相交区域面积的近似值可k/n。
使相交区域对象素亮度的贡献依赖于该区域与象素中心的距离,当直线经过该像素时,该像素的亮度F是在两者相交区域A’上对滤波器(函数w)进行积分的积分值:
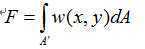
滤波器函数w可以取高斯滤波器:
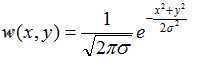
如:我们将屏幕划分为n=3×3个子象素,加权表可以取作:
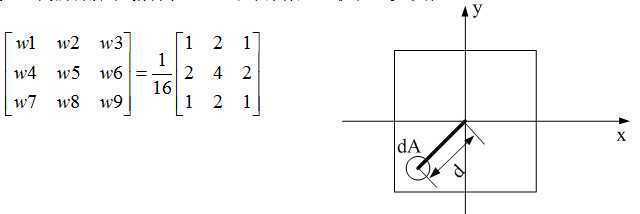
权函数w(x,y)为微面dA与像素中心距离d的函数,然后求出所有中心落于直线段内的子像素,最后计算出所有这些子像素对原像素亮度贡献之和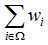 乘以像素的最大灰度值作为该像素的显示灰度值。
乘以像素的最大灰度值作为该像素的显示灰度值。
特别地,当每个权值都相等时,加权区域采样就退化为非加权区域采样。
确定图形中哪些部分落在显示区域之内,哪些落在显示区域之外,显示器只显示落在显示区域内的图形。这个过程称为裁剪。
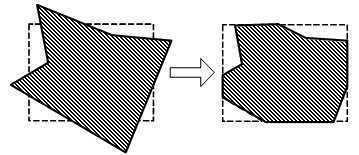
对于每条线段P1P2分为三种情况处理:
(1)若P1P2完全在窗口内,则显示该线段
(2)若P1P2明显在窗口外,则丢弃该线段
(3)若线段不满足“取”或 “弃”的条件,则在交点处把线段分为两段。其中一段完全在窗口外,可弃之。然后对另一段重复上述处理。
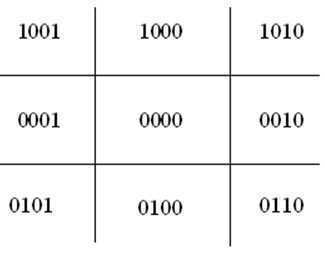
为了快速判断采用编码方法:每个区域赋予4位编码:
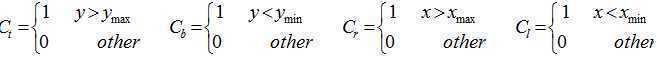
若P1P2完全在窗口内code1=0,且code2=0,则“取”
若P1P2明显在窗口外code1&code2≠0,则“弃”
在交点处把线段分为两段。其中一段完全在窗口外,可弃之。然后对另一段重复上述处理
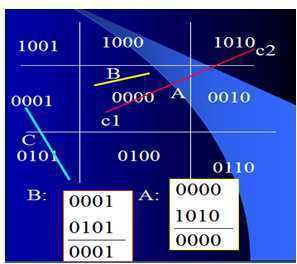
C1=C2=0 线段在窗口内,线段直接接收(B线段)。
C1&C2!=0 线段在窗口外,线段直接舍弃(C线段) 。
C1&C2=0 线段与窗口有交点(A线段)
当一条线断不能直接接受也不能直接舍弃时,则将其线段拆成一半,再并分别测试线段,通过二分法搜索方式直至线段被接受,如图所示:
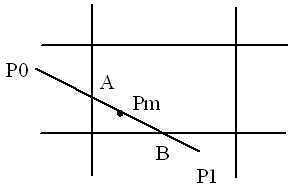
A、B分别为距P0、P1最近的可见点,Pm为P0P1中点。
中点分割裁剪法优点:计算速度快,因为算法简单,算法只需作位移计算。
从P0出发找最近可见点采用中点分割方法
先求出P0P1的中点Pm
若P0Pm不是显然不可见的,并且P0P1在窗口中有可见部分,则距P0最近的可见点一定落在P0Pm上,所以用P0Pm代替P0P1
否则取PmP1代替P0P1
再对新的P0P1求中点Pm。重复上述过程,直到PmP1长度小于给定的控制常数为止,此时Pm收敛于交点
从P1出发找最近可见点采用上面类似方法。
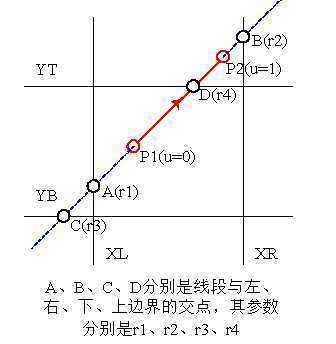
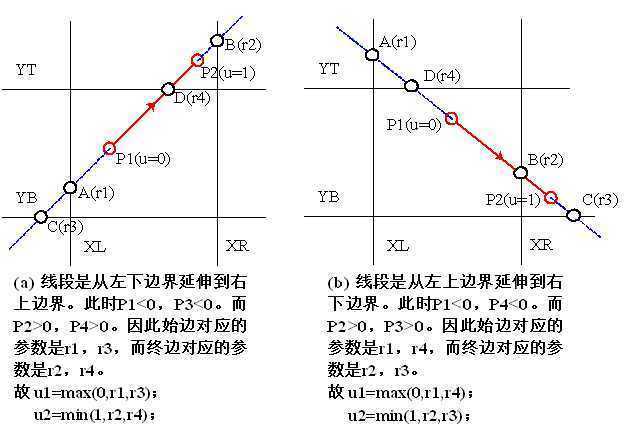
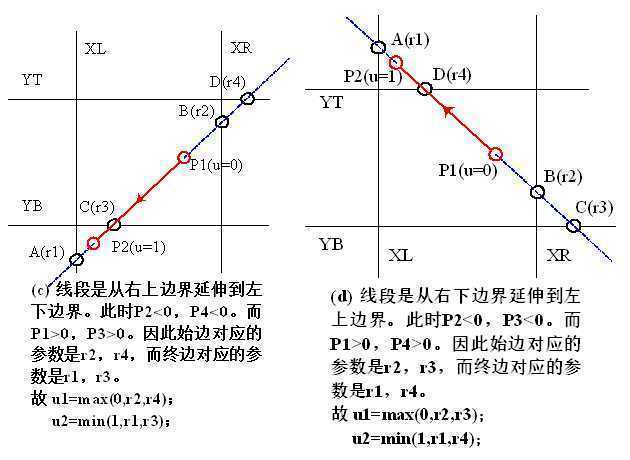
将线段P1P2表示为参数形式:
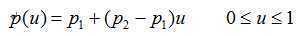
确定始边和终边:左→右,右→左,下→上,上→下。
两组交点:1、与始边交点A和C,参数为r1和r3;2、与终边交点B和D,参数为r2和r4。
裁剪矩形内的先端部分由参数u1和u2定义:u1 = max(0,r1,r3);u2 = max(1,r2,r4)。
两个问题:1、如何确定始边和终边?2、怎样求r1,r2,r3,r4?
解决方法:
线段的参数化形式
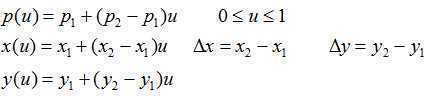
参数化形式的裁剪条件
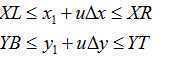
第一个问题:求解线段与左、右、下、上边界的交点参数r1,r2,r3和r4。
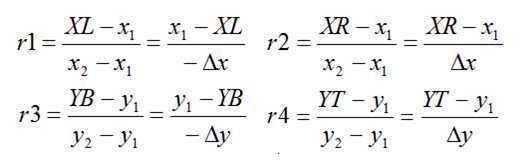
可统一表示为:
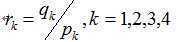
其中:
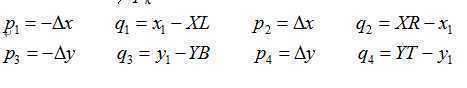
第二个问题:如何确定始边和终边?
特殊情况:
当pk=0且qk<0,
则线段完全在边界外,qk≥0,则该线段平行于裁剪边界并且在窗口内
当pk≠0时
对于每条直线,裁剪矩形内的线段部分由参数u1和u2定义
多边形裁剪结果仍是一个或多个多边形。
多边形裁剪重点考虑问题:把多边形落在窗口边界上的交点正确地按序连接成裁剪后的多边形(其中包括决定窗口边界及拐角的取舍)。
每次用窗口的一条变界对要裁剪的多边形进行裁剪,把落在窗口外部区域的图形去掉,保留窗口内部区域的图形,并把它作为下一次待裁剪的多边形。
1).指定多边形的顶点序列P
2).取一条窗口裁剪多边形的边e依次检查顶点序列种的每个顶点p[I]。
并由下面的判断:
a.处于e边可见侧被列入新产生的顶点序列Q[j]中。
b.处于e边不可见侧的顶点则被删除。
3)检查p[I]与p[i+1]是否处于同则,若不是则求交点,求得的交点列入新多边形顶点序列Q[j]中。如图所示:
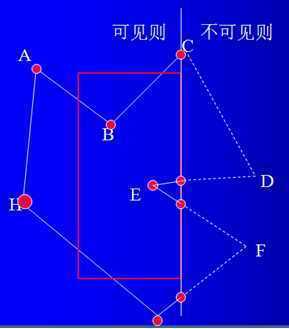
4)取裁剪窗口的右边界为裁剪边,则有新顶点序列由红色的点组成。
5)依次再用底边、左边和顶边分别对作裁剪。最终获得裁剪后的多边形。
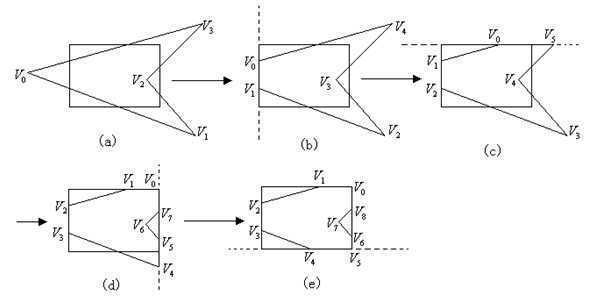
设用户的多边型为主多边形ps,而裁剪窗口为裁剪多边形pc.
算法首先沿ps任一点出发,各跟踪检测ps的每一条边,当ps与pc的有效边相交时:
(1)若ps的边进入pc,则继续沿ps的边往下处理,并输出
(2)若ps的边是从pc中出来,则从该点(称为前交点)开始,沿着窗口边向右检测pc的边,找到ps与pc最靠近的前交点的新交点。同时输出由前交点到新交点的线段。
(3)返回到前交点,继续(1)~ (3)的步骤。
主多边形和裁剪多边形把二维平面分成两部分
内裁剪:A∩B
外裁剪:A-B
裁剪结果区域的边界由A的部分边界和B的部分边界两部分构成,并且在交点处边界发生交替,即由A的边界转至B的边界,或由B的边界转至A的边界 。
原文:http://www.cnblogs.com/tgycoder/p/5127985.html