LCA的tarjan求法&&POJ 1470的辛酸历程

转载请注明出处：http://blog.csdn.net/jiangshibiao/article/details/23659735

【LCA的线性解法】LCA（最近公共祖先）的问题十分常见。以前我单纯的认为，每次O(N)扫一遍每个节点的深度、再直接暴力求LCA的效率很高——Nlog(N)。但是往往树会退化成链（或者说它不平衡），如果询问次数多的话肯定TLE。离线解法TARJAN（这人好厉害，强连通算法也是他发明的）的效率则是O(N+Q)，其中Q是询问个数。

【原理】用到了并查集的思想，每次对于一个点，处理询问中与他有关的一些点，最后链到它的父亲中。递归实现。

【伪代码】

【原题】

Description

Input

Output

For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times 
For example, for the following tree: 

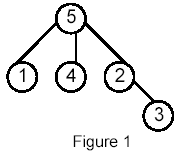
Sample Input

5
5:(3) 1 4 2
1:(0)
4:(0)
2:(1) 3
3:(0)
6
(1 5) (1 4) (4 2)
      (2 3)
(1 3) (4 3)

Sample Output

2:1
5:5

Hint

Source

【大意】给定一棵树的结构和一些询问（x，y），求x和y的LCA。输出每个点它成为多少点对的答案。

【初始代码】

#include<cstdio>
#define N 1005
using namespace std;
char ch;
struct arr{int next,go;}a[N*2];
struct ARR{int NEXT,GO;}A[N*2];
int f[N],x,y,num,n,m,i,ans[N],cnt,CNT,end[N],END[N],root;
bool visit[N],flag[N*2];
inline int Read()
{
  while (ch<‘0‘||ch>‘9‘) ch=getchar();int s=0;
  while (ch>=‘0‘&&ch<=‘9‘) s=s*10+ch-48,ch=getchar();return s;
}
inline void add(int u,int v) {a[++cnt].go=v;a[cnt].next=end[u];end[u]=cnt;}
inline void ADD(int U,int V) {A[++CNT].GO=V;A[CNT].NEXT=END[U];END[U]=CNT;}
inline int get(int u){return f[u]==u?u:f[u]=get(f[u]);}
void tarjan(int k)
{
  f[k]=k;visit[k]=true;
  for (int i=end[k];i>=0;i=a[i].next)
  {
    int go=a[i].go;
    if (!visit[go])
    {
      tarjan(go);f[go]=k;
    }
  }
  for (int i=END[k];i>=0;i=A[i].NEXT)
  {
    int GO=A[i].GO;
    if (visit[GO]&&!flag[i]) ans[get(GO)]++,flag[i]=true,flag[i^1]=true;
  }
}
int main()
{
  scanf("%d",&n);ch=‘ ‘;cnt=CNT=-1;
  for (i=1;i<=n;i++) end[i]=END[i]=-1;
  for (i=1;i<=n;i++)
  {
    x=Read();num=Read();if (i==1) root=x;
    while (num)
    {
      num--;y=Read();add(x,y);add(y,x);
    }
  }
  m=Read();
  for (i=1;i<=m;i++)
    x=Read(),y=Read(),ADD(x,y),ADD(y,x);
  tarjan(root);
  for (i=1;i<=n;i++)
    if (ans[i]) printf("%d:%d\n",i,ans[i]);
  return 0;  
}

【悲惨经历】几乎什么问题都被我碰上了。

【注意点】

①给定的是有向边。

②根要自己找。我一开始以为是无向边，这样无法获取根的位置，于是我默认第一个输入的点是根~~

③读入注意一下。（我觉得我的读入优化应该没问题，虽然AC代码中改成了scanf）

④有些时候会重复计算。因为是有向边，我们可以把visit[k]=true移到中间，这样就不会重复计算了。（当然麻烦点也可以，我原来是开边表的，多开一个bool数组判重也可以）

⑤英语渣，没看出来——有多组数据。

⑥因为有多组数据，所以每次要好好的清零。

以上的改好后，我就一直RE，后来去网上找题解，它们说询问要用邻接矩阵来记录。为什么呢？原来可能有多次重复询问（这题目太坑了，竟然没说询问个数）或者询问的很多，邻接矩阵还能记录重复的询问。

最终，A掉了。真是感慨万千啊！

【AC代码】

#include<cstdio>
#include<cstring>
#define N 1005
using namespace std;
char ch;
struct arr{int next,go;}a[N*2];
int f[N],x,y,num,n,m,i,ans[N],cnt,CNT,end[N],END[N],root,fa[N],ask[N][N];
bool visit[N];
inline void add(int u,int v) {a[++cnt].go=v;a[cnt].next=end[u];end[u]=cnt;}
inline int get(int u){return f[u]==u?u:f[u]=get(f[u]);}
void tarjan(int k)
{
  f[k]=k;
  for (int i=end[k];i;i=a[i].next)
  {
    int go=a[i].go;
    tarjan(go);f[go]=k;
  }
  visit[k]=true;
  for (int i=1;i<=n;i++)
    if (visit[i]&&ask[k][i])
      ans[get(i)]+=ask[k][i];

}
int main()
{
  while (scanf("%d",&n)!=EOF)
  {
    memset(end,0,sizeof(end));
    memset(ask,0,sizeof(ask));
    memset(ans,0,sizeof(ans));
    memset(fa,0,sizeof(fa));
    memset(visit,0,sizeof(visit));
    cnt=0;CNT=0;
    for (i=1;i<=n;i++)
    {
      scanf("%d:(%d)",&x,&num);
      while (num)
      {
        num--;scanf("%d",&y);add(x,y);fa[y]++;
      }
    }
    scanf("%d",&m);
    for (i=1;i<=m;i++)
      scanf(" (%d %d) ",&x,&y),ask[x][y]++,ask[y][x]++;
    for (i=1;i<=n;i++)
      if (fa[i]==0) {root=i;break;}
    tarjan(root);
    for (i=1;i<=n;i++)
      if (ans[i]) printf("%d:%d\n",i,ans[i]);
  }
  return 0;  
}

LCA的tarjan求法&&POJ 1470的辛酸历程,布布扣,bubuko.com

LCA的tarjan求法&&POJ 1470的辛酸历程

原文：http://blog.csdn.net/jiangshibiao/article/details/23659735