高斯分布
\[\mathcal{N}(x|\mu,\sigma ^2)=\frac{1}{(2\pi\sigma ^2)^{1/2}}exp\left\{-\frac{1}{2\sigma ^2}(x-\mu)^2\right\}\]
多维高斯分布
\[\mathcal{N}(\mathbf{x}|\mathbf{\mu},\mathbf{\Sigma})=\frac{1}{(2\pi)^{D/2}|\mathbf{\Sigma}|^{1/2}}exp\left\{-\frac{1}{2}(\mathbf{x}-\mathbf{\mu})^{T}\mathbf{\Sigma}^{-1}(\mathbf{x}-\mathbf{\mu})\right\}\]
\(\mathbf{x}=(x_1,\ldots ,x_N)^T\)是对变量\(x\)的\(N\)个观测,每个观测都是独立从同一高斯分布中抽样的,独立同分布,所以得到一个观测的概率可以表示为
\[p(\mathbf{x}|\mu,\sigma ^2)=\prod_{n=1}^N\mathcal{N}(x_n|\mu,\sigma ^2)\]
这是似然函数,是关于\(\mu,\sigma ^2\)的函数,通过极大化似然函数可以求得参数,极大似然法寻找一组参数使得所观测的概率最大,挺奇怪的
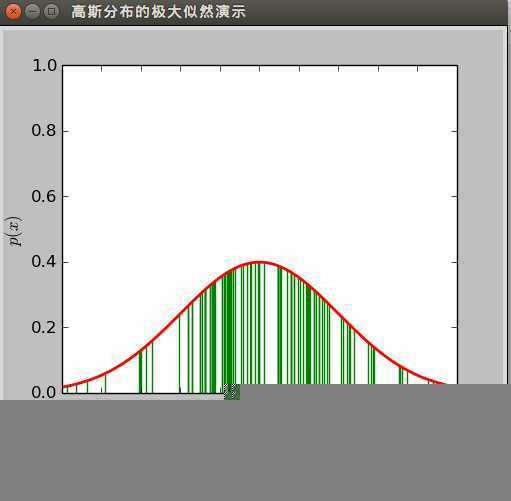
x轴上的点是观测值,绿色的线长度表示观测值的概率密度,所有绿线的长度相乘,得到观测值的概率密度,通过调整参数\(\mu,\sigma ^2\)使得这个乘积最大,这是极大似然法的思想
python+matplotlib+tkinter实现演示:

1 import numpy as np 2 import matplotlib 3 import matplotlib.pyplot as plt 4 import random 5 from Tkinter import * 6 from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg 7 from matplotlib.figure import Figure 8 9 N = 100 #采样点数目 10 mu = 0.5 #采样均值 11 sigma = 1 #采样标准差 12 13 x0 =np.linspace(-2,3,200,endpoint=True) #高斯分布画图点 14 x = np.random.normal(loc=mu, scale=sigma, size=N) #高斯分布采样 15 t1 = np.mean(x) #最大似然均值 16 t2 = np.sqrt(np.mean(np.square(x-t1))) #最大似然标准差 17 leftlim = -2 #横坐标左极限 18 rightlim = 3 #横坐标右极限 19 20 #高斯分布 21 def gaussian(x,mu,sigma): 22 return 1/(2*np.pi*sigma**2)**(0.5)*np.exp(-1/(2*sigma**2)*(x-mu)**2) 23 #滑块sc1和sc2回调函数 24 def draw_pic(self): 25 #获得均值和标准差参数 26 try:mu = float(v1.get()) 27 except: 28 mu = 0.5 29 sc1.set(mu) 30 try:sigma = float(v2.get()) 31 except: 32 sigma = 1 33 sc2.set(sigma) 34 #清除图像 35 draw_pic.f.clf() 36 #画图 37 draw_pic.a = draw_pic.f.add_subplot(111) 38 draw_pic.a.set_xlim(leftlim,rightlim) 39 draw_pic.a.set_ylim(0,1) 40 draw_pic.a.set_xlabel(r‘$x$‘) 41 draw_pic.a.set_ylabel(r‘$p(x)$‘) 42 draw_pic.a.set_xticks(np.arange(leftlim,rightlim,0.5).tolist()) 43 x0 =np.linspace(leftlim,rightlim,200,endpoint=True) 44 draw_pic.a.plot(x0,gaussian(x0,mu,sigma),color=‘r‘,linewidth=2) 45 draw_pic.a.vlines(x.tolist(),[0],gaussian(x,mu,sigma).tolist(),color=‘g‘) 46 draw_pic.canvas.show() 47 #设置标签 48 lb1.configure(text = "mu_ML:"+t1.astype(‘str‘)+ 49 "\nsigma_ML:"+t2.astype(‘str‘) 50 +"\nSum of log of gaussian of x_n: "51 +np.sum(np.log(gaussian(x,mu,sigma))).astype(‘|S10‘)) 52 53 54 if __name__ == ‘__main__‘: 55 56 matplotlib.use(‘TkAgg‘) 57 root = Tk() 58 59 draw_pic.f = Figure(figsize=(5,4),dpi=100) 60 draw_pic.canvas = FigureCanvasTkAgg(draw_pic.f,master = root) 61 draw_pic.canvas.show() 62 draw_pic.canvas.get_tk_widget().grid(row = 0,columnspan = 3) 63 #标签 64 lb1 = Label(root, text="") 65 lb1.grid(row=1,column=0) 66 #滑块1,用于设定均值 67 v1 = StringVar() 68 sc1 = Scale(root, 69 from_ = 0, 70 to = 1, 71 resolution = 0.001, 72 orient = HORIZONTAL, 73 variable = v1 , 74 label = ‘mu:‘ , 75 command = draw_pic 76 ) 77 sc1.grid(row=1,column=1) 78 sc1.set(0.5) 79 #滑块2,用于设定标准差 80 v2= StringVar() 81 sc2 = Scale(root, 82 from_ = 0.000001, 83 to = 3, 84 resolution = 0.001, 85 orient = HORIZONTAL, 86 variable = v2 , 87 label = ‘sigma:‘ , 88 command = draw_pic 89 ) 90 sc2.grid(row=1,column=2) 91 sc2.set(1) 92 93 root.mainloop()
原文:http://www.cnblogs.com/wangsirui/p/5136608.html