布尔莎七参数的数学模型为
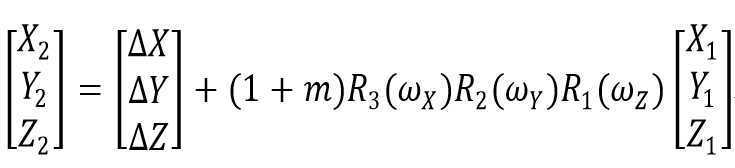[X1，Y1，Z1]为待求坐标，[X2，Y2，Z2]为目标坐标系坐标。顾及旋转角度都是非常小的，布尔莎七参数转换模型的数学模型可以简化为：
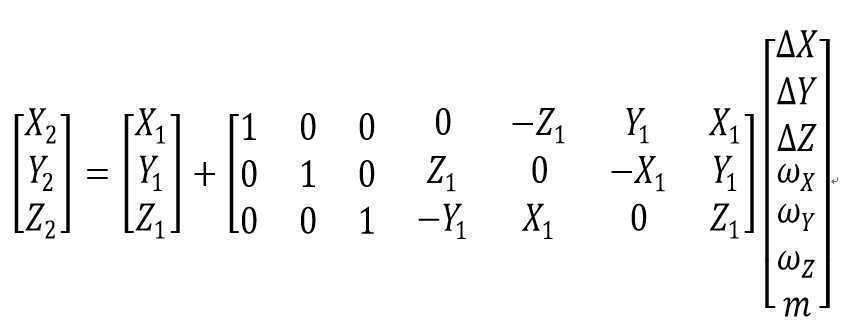这样有利于使用编程语言来求解。由公式可知，必要观测条件数为 t=7, 所以至少需要3个已知点对。设已知点对数为m，则多余观测数 r = 3*m - 7, 这在最终的精度评定中是有用的。
1. 由于是同等精度观测且相互独立，最终使用的权阵应该为单位矩阵 P(3m*3m), m为已知点对个数。
p = np.eye(n) # 单位权矩阵 3n * 3n
2. 程序实现时，所有的已知点对XYZ坐标都读入相应的列矩阵，系数阵B同样需要这样操作（V=BX-L)。在numpy处理时可以表示为：
1 for i in range(vector_count): 2 matrix_source.append(vector3d_list_source[i].X) 3 matrix_source.append(vector3d_list_source[i].Y) 4 matrix_source.append(vector3d_list_source[i].Z) 5 matrix_dest.append(vector3d_list_dest[i].X) 6 matrix_dest.append(vector3d_list_dest[i].Y) 7 matrix_dest.append(vector3d_list_dest[i].Z) 8 matrix_B.append([1, 0, 0, 0, -vector3d_list_source[i].Z, vector3d_list_source[i].Y, vector3d_list_source[i].X]) 9 matrix_B.append([0, 1, 0, vector3d_list_source[i].Z, 0, -vector3d_list_source[i].X, vector3d_list_source[i].Y]) 10 matrix_B.append([0, 0, 1, -vector3d_list_source[i].Y, vector3d_list_source[i].X, 0, vector3d_list_source[i].Z]) 11 matrix_source = np.array(matrix_source).reshape(1, -1).T 12 matrix_dest = np.array(matrix_dest).reshape(1, -1).T 13 matrix_B = np.array(matrix_B) 14 L = matrix_dest - matrix_source
3. 参数矩阵值（列矩阵）
X = np.dot(np.linalg.inv(np.dot(matrix_B.T, matrix_B)), np.dot(matrix_B.T, L))
4. 误差方程
V = np.dot(matrix_B, X) - L #误差方程
5. 精度评估
standard_deviation = math.sqrt(np.dot(np.dot(V.T, p), V) / r) # 转换中误差
原文：http://www.cnblogs.com/AllStarGIS/p/5143206.html