相似矩阵

定义

特征值的一个重要应用是，他能将A进行对角化，得到：\( \Lambda =S^{-1}A S \)（假如存在S逆的话）。如果我们将S替换为一般的矩阵M（存在逆矩阵），得到：\( B=M^{-1}AM \)，我们说B与A相似（当然A与B也相似，相似是相互的）。当然，A与Λ是相似的。

相似矩阵的特征值相同

为什么要讨论相似矩阵？因为我们要带出一个重要结论：相似矩阵的特征值相同（但特征向量不同，见下）。

证明很简单:

• 对角矩阵应该是相似矩阵中的明星，因为它的特征值就在对角线上，特征向量是（1,0），（0,1）（拿二维打个比方）
• 上三角矩阵也是重要一员，它的特征值也在对角线上，不过它的特征向量没这么容易看出来。

当A的特征值相同时

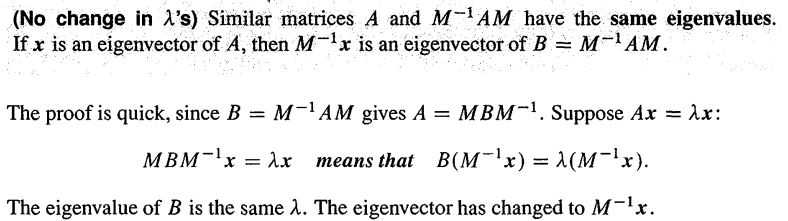
美好的愿望：我们似乎能将相似矩阵归为一个大family，family中的矩阵两两之间相互相似（拥有相同特征值），可以通过Λ将他们连接起来。我们可以证明相似的传递性：

假设\( B=M^{-1}\Lambda M \)，\( C=N^{-1}\Lambda N \)，

那么\( C=N^{-1}M\Lambda M^{-1}N=(M^{-1}N)^{-1}\Lambda (M^{-1}N) \)，证毕。

残酷的现实：遗憾的是，当集合中特征值相同时，具有相同特征值的矩阵集合这个大family分为两个小family：

• 其一只包含对角矩阵：λI
• 其二是其余所有矩阵，一个代表是上三角矩阵，对角线元素是λ，上三角随便填什么数都行

这两个family有以下特点：

• 第一个矩阵永远无法与第二族矩阵相似，第一个矩阵只能与他自己相似，因为对任何M，都有M^-1λIM=λI
• 第二个family中的矩阵无法对角化（假如能对角化，它们就需要与第一个矩阵相似，这是不可能的）

Jordan form与Jordan matrix

当矩阵所有特征值相同时，将上三角紧贴对角线的元素以1填充，得到的矩阵叫做Jordan form，由这些Jordan form在对角线上构成的矩阵叫做Jordan Matrix（见图）。

• Jordan Matrix的特征向量个数=块的个数（因为每个块内特征值相同，带出的特征向量也相同）
• 可以证明任何方阵A都与某个Jordan Matrix相似（这个证明，以及给出A求Jordan Matrix的过程都不容易，此处略过）
• 如果矩阵没有重复的特征值，那么Jordan Matrix退化为对角矩阵Λ，这也是我们所期望的结果。

线性代数学习笔记（十四）,布布扣,bubuko.com

线性代数学习笔记（十四）

原文：http://www.cnblogs.com/ericxing/p/3665002.html