归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并排序的基本思想
将待排序序列R[0...n-1]看成是n个长度为1的有序序列,将相邻的有序表成对归并,得到n/2个长度为2的有序表;将这些有序序列再次归并,得到n/4个长度为4的有序序列;如此反复进行下去,最后得到一个长度为n的有序序列。
归并操作
归并操作(merge),也叫归并算法,指的是将两个顺序序列合并成一个顺序序列的方法。
如 设有数列{6,202,100,301,38,8,1}
初始状态:6,202,100,301,38,8,1
第一次归并后:{6,202},{100,301},{8,38},{1},比较次数:3;
第二次归并后:{6,100,202,301},{1,8,38},比较次数:4;
第三次归并后:{1,6,8,38,100,202,301},比较次数:4;
总的比较次数为:3+4+4=11,;
逆序数为14;
算法描述
归并操作的工作原理如下:
第一步:申请空间,使其大小为两个已经
排序序列之和,该空间用来存放合并后的序列
第二步:设定两个
指针,最初位置分别为两个已经排序序列的起始位置
第三步:比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
重复步骤3直到某一指针超出序列尾
将另一序列剩下的所有元素直接复制到合并序列尾
综上可知:
归并排序其实要做两件事:
(1)“分解”——将序列每次折半划分。
(2)“合并”——将划分后的序列段两两合并后排序。
我们先来考虑第二步,
public void Merge(int[] array, int low, int mid, int high) {
int i = low; // i是第一段序列的下标
int j = mid + 1; // j是第二段序列的下标
int k = 0; // k是临时存放合并序列的下标
int[] array2 = new int[high - low + 1]; // array2是临时合并序列
// 扫描第一段和第二段序列,直到有一个扫描结束
while (i <= mid && j <= high) {
// 判断第一段和第二段取出的数哪个更小,将其存入合并序列,并继续向下扫描
if (array[i] <= array[j]) {
array2[k] = array[i];
i++;
k++;
} else {
array2[k] = array[j];
j++;
k++;
}
}
// 若第一段序列还没扫描完,将其全部复制到合并序列
while (i <= mid) {
array2[k] = array[i];
i++;
k++;
}
// 若第二段序列还没扫描完,将其全部复制到合并序列
while (j <= high) {
array2[k] = array[j];
j++;
k++;
}
// 将合并序列复制到原始序列中
for (k = 0, i = low; i <= high; i++, k++) {
array[i] = array2[k];
}
}
在某趟归并中,设各子表的长度为gap,则归并前R[0...n-1]中共有n/gap个有序的子表:R[0...gap-1], R[gap...2*gap-1], ... , R[(n/gap)*gap ... n-1]。
调用Merge将相邻的子表归并时,必须对表的特殊情况进行特殊处理。
若子表个数为奇数,则最后一个子表无须和其他子表归并(即本趟处理轮空):若子表个数为偶数,则要注意到最后一对子表中后一个子表区间的上限为n-1。

public void MergePass(int[] array, int gap, int length) {
int i = 0;
// 归并gap长度的两个相邻子表
for (i = 0; i + 2 * gap - 1 < length; i = i + 2 * gap) {
Merge(array, i, i + gap - 1, i + 2 * gap - 1);
}
// 余下两个子表,后者长度小于gap
if (i + gap - 1 < length) {
Merge(array, i, i + gap - 1, length - 1);
}
}
public int[] sort(int[] list) {
for (int gap = 1; gap < list.length; gap = 2 * gap) {
MergePass(list, gap, list.length);
}
return list;
}
算法分析
归并排序算法的性能
| 排序类别 |
排序方法 |
时间复杂度 |
空间复杂度 |
稳定性 |
复杂性 |
| 平均情况 |
最坏情况 |
最好情况 |
| 归并排序 |
归并排序 |
O(nlog2n) |
O(nlog2n) |
O(nlog2n) |
O(n) |
稳定 |
较复杂 |
时间复杂度
归并排序的形式就是一棵二叉树,它需要遍历的次数就是二叉树的深度,而根据完全二叉树的可以得出它的时间复杂度是O(n*log2n)。
空间复杂度
由前面的算法说明可知,算法处理过程中,需要一个大小为n的临时存储空间用以保存合并序列。
在归并排序中,相等的元素的顺序不会改变,所以它是稳定的算法。
若从空间复杂度来考虑:首选堆排序,其次是快速排序,最后是归并排序。
若从稳定性来考虑,应选取归并排序,因为堆排序和快速排序都是不稳定的。
若从平均情况下的排序速度考虑,应该选择快速排序。
完整实现
以下代码可以直接运行。


public class MergeSort {
public void Merge(int[] array, int low, int mid, int high) {
int i = low; // i是第一段序列的下标
int j = mid + 1; // j是第二段序列的下标
int k = 0; // k是临时存放合并序列的下标
int[] array2 = new int[high - low + 1]; // array2是临时合并序列
// 扫描第一段和第二段序列,直到有一个扫描结束
while (i <= mid && j <= high) {
// 判断第一段和第二段取出的数哪个更小,将其存入合并序列,并继续向下扫描
if (array[i] <= array[j]) {
array2[k] = array[i];
i++;
k++;
} else {
array2[k] = array[j];
j++;
k++;
}
}
// 若第一段序列还没扫描完,将其全部复制到合并序列
while (i <= mid) {
array2[k] = array[i];
i++;
k++;
}
// 若第二段序列还没扫描完,将其全部复制到合并序列
while (j <= high) {
array2[k] = array[j];
j++;
k++;
}
// 将合并序列复制到原始序列中
for (k = 0, i = low; i <= high; i++, k++) {
array[i] = array2[k];
}
}
public void MergePass(int[] array, int gap, int length) {
int i = 0;
// 归并gap长度的两个相邻子表
for (i = 0; i + 2 * gap - 1 < length; i = i + 2 * gap) {
Merge(array, i, i + gap - 1, i + 2 * gap - 1);
}
// 余下两个子表,后者长度小于gap
if (i + gap - 1 < length) {
Merge(array, i, i + gap - 1, length - 1);
}
}
public int[] sort(int[] list) {
for (int gap = 1; gap < list.length; gap = 2 * gap) {
MergePass(list, gap, list.length);
System.out.print("gap = " + gap + ":\t");
this.printAll(list);
}
return list;
}
// 打印完整序列
public void printAll(int[] list) {
for (int value : list) {
System.out.print(value + "\t");
}
System.out.println();
}
public static void main(String[] args) {
int[] array = { 9, 1, 5, 3, 4, 2, 6, 8, 7};
MergeSort merge = new MergeSort();
System.out.print("排序前:\t\t");
merge.printAll(array);
merge.sort(array);
System.out.print("排序后:\t\t");
merge.printAll(array);
}
}
归并排序之JAVA实现
运行结果
排序前: 9 1 5 3 4 2 6 8 7
gap = 1: 1 9 3 5 2 4 6 8 7
gap = 2: 1 3 5 9 2 4 6 8 7
gap = 4: 1 2 3 4 5 6 8 9 7
gap = 8: 1 2 3 4 5 6 7 8 9
排序后: 1 2 3 4 5 6 7 8 9
自底向上的归并排序
一. 算法描述
自底向上的归并排序:归并排序主要是完成将若干个有序子序列合并成一个完整的有序子序列;自底向上的排序是归并排序的一种实现方式,将一个无序的N长数组切个成N个有序子序列,然后再两两合并,然后再将合并后的N/2(或者N/2 + 1)个子序列继续进行两两合并,以此类推得到一个完整的有序数组。下图详细的分解了自底向上的合并算法的实现过程:
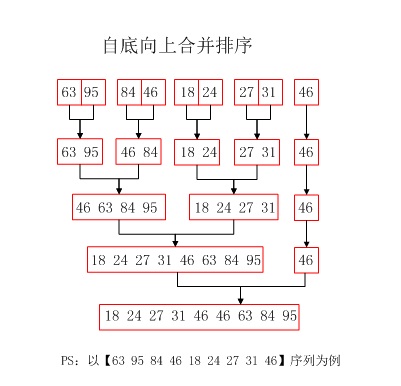
二. 算法分析
平均时间复杂度:O(nlog2n)
空间复杂度:O(n) (用于存储有序子序列合并后有序序列)
稳定性:稳定
三. 算法实现
- void Merge(int* pDataArray, int *pTempArray, int bIndex, int mIndex, int eIndex)
- {
- int mLength = eIndex - bIndex;
- int i = 0;
- int j = bIndex;
- int k = mIndex;
-
- while (j < mIndex && k < eIndex)
- {
- if (pDataArray[j] <= pDataArray[k])
- {
- pTempArray[i++] = pDataArray[j];
- j++;
- }
- else
- {
- pTempArray[i++] = pDataArray[k];
- k++;
- }
- }
-
- if (j == mIndex)
- while (k < eIndex)
- pTempArray[i++] = pDataArray[k++];
- else
- while (j < mIndex)
- pTempArray[i++] = pDataArray[j++];
-
- for (i = 0; i < mLength; i++)
- pDataArray[bIndex + i] = pTempArray[i];
- }
-
- void BottomUpMergeSort(int* pDataArray, int iDataNum)
- {
- int *pTempArray = (int *)malloc(sizeof(int) * iDataNum);
- int length = 1;
- while (length < iDataNum)
- {
- int i = 0;
- for (; i + 2*length < iDataNum; i += 2*length)
- Merge(pDataArray, pTempArray, i, i + length, i + 2*length);
- if (i + length < iDataNum)
- Merge(pDataArray, pTempArray, i, i + length, iDataNum);
- length *= 2;
- }
- free(pTempArray);
- }
归并排序
原文:http://www.cnblogs.com/nxxshxf/p/5151354.html



