本次我们将提出另一种设计线性分类器的原理。我们将从二类线性可分的任务开始,然后将这种方法扩展到数据不可分的更一般的情形。
让 $x_i,i=1,2,\ldots,N$,表示训练集X的特征向量,这些向量属于两类中的任意一类,并且假设这些向量是线性可分的,目标还是设计一个超平面:
$$g(x)=w^Tx+w_0=0$$
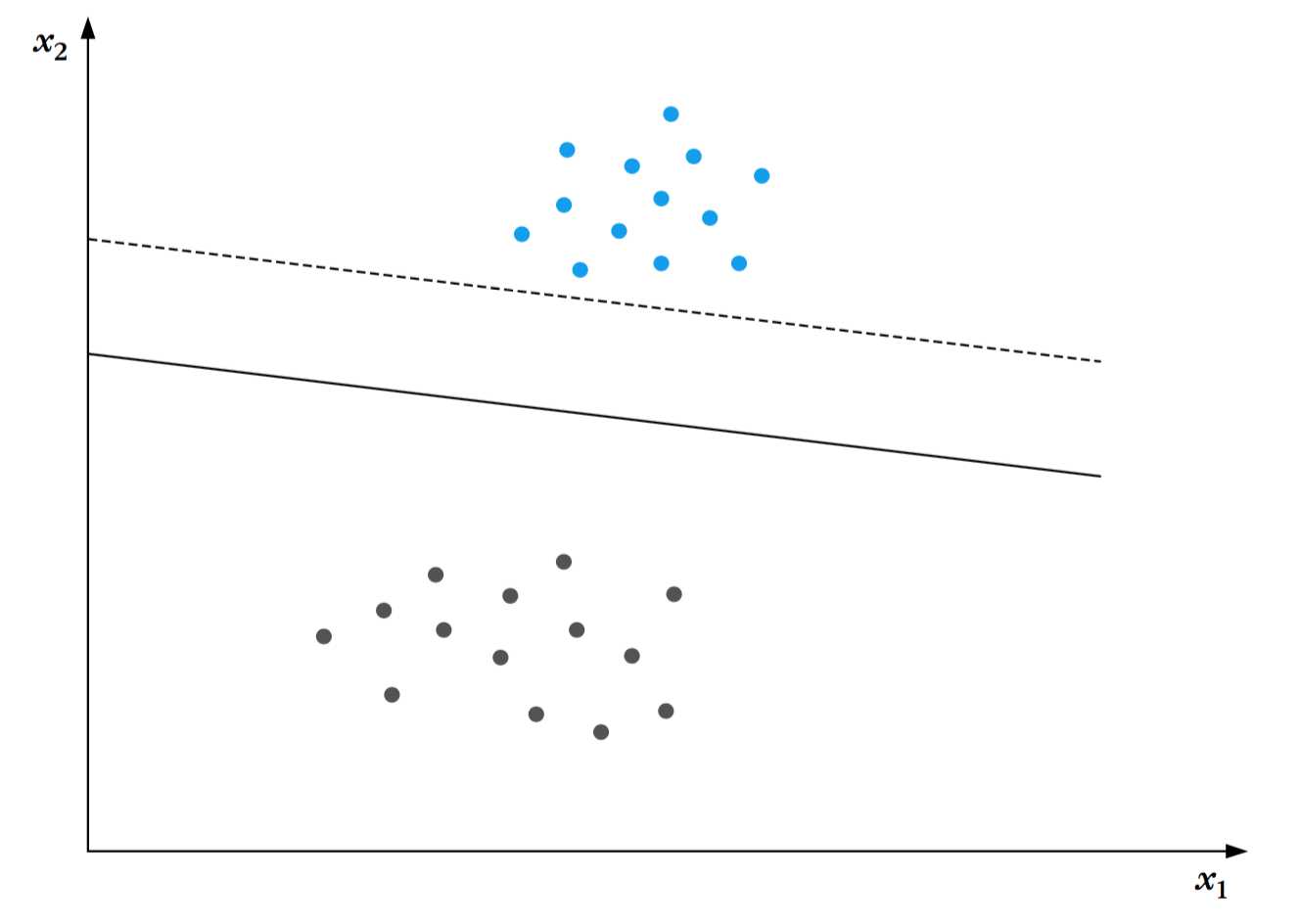
使该超平面可以将所有的训练数据正确分类。由于这样的一个超平面并不是唯一的。根据已有的经验,感知机算法会收敛到任意一个可能的解,这次我们希望更加严苛。下图阐明了分类任务的两个可能的超平面的解。两个超平面都完成了对训练集分类的任务。然而,在实践中,训练集以外的数据将会被送到分类器中,一个敏锐的工程师将选择这两个超平面中的哪一个作为分类器呢?毫无疑问答案是实线表示的分类器,原因是这个超平面为两边都留了更多的空间,使得两类中的数据都可以更加自由的移动,而产生错误的风险更小。当它面对处理未知数据的挑战时,这样的一个超平面更加被信服。此时我们遇到了在分类器设计阶段一个非常重要的问题,它被称为“分类器的通用性能”,这涉及到分类器的性能问题,分类器使用训练数据集设计,用来正确地处理训练集以外的数据。
原文:http://www.cnblogs.com/lengyue365/p/5181106.html