转载请注明出处：http://www.cnblogs.com/ymingjingr/p/4271742.html
三学习原则。
奥卡姆剃刀定律。
entia non sunt multiplicanda praeter necessitatem（此处是拉丁文…），译为英文是entities must not be multiplied beyond necessity，意思是如无必要，勿增实体，出自奥卡姆，为了纪念此人，将这句话叫做奥卡姆剃刀（Occam‘s Razor）。
将奥卡姆剃刀定律应用在机器学习上意思是使用的模型尽可能的简单。如图16-1所示，对于同一组数据集，两种不同的分类模型，应该如何选择？
图16-1 不同模型的选择
通过肉眼观察，当然会选择左边的图形，因为它简单，于是产生了两个问题，什么情况意味着模型是简单的？如何得知简单的模型会有好的表现？
先从第一个问题着手，简单意味着什么。
对于一个假设h，参数越小意味着越简单，如图16-1中，左图只需要极少的参数，如圆心和半径。
对于一个假设空间H，有效的假设数量越少则意味着越简单。
两者之间有何联系？两者是密切相关的，如一个假设空间H的假设数量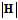
为
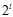，则单一的假设可用
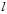bits表示。因此如果假设空间H的模型是简单的（
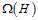很小），则处在此假设空间中的假设h也是简单的（
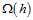很小）。
接着使用一个直觉上的解释阐述为什么越简单的模型会有越好的效果。
假设一个数据集的规律性很差，如输入样本的输出标记都是随便标记的，此种情况，很少有甚至没有假设函数能使得该样本的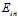
等于0。如果一个数据集能被某模型分开，则该数据集的规律性不会特别差。在使用简单模型将某数据集大致区分开时，则可以确定该数据集是具有某种规律性的；如果是用复杂模型将某数据集分开，则无法确定是数据集具有规律性还是模型足够复杂恰巧将混乱的数据集分离。
因此，在运用模型时，先使用简单的模型，一般使用最简单的线性模型。
抽样偏差。
如果数据的抽样出现偏差，则机器学习也会产生偏差，此种偏差称为抽样偏差（sampling bias）。
对上述结论用一个技术性的说明：在VC理论中，其中一个假设是训练样本和测试样本以同样的概率来自于同一个数据分布。因此在训练数据来自于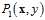
，而测试样本的概率
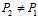时，VC理论无法适用，即
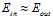不成立。
这就好比，当你数学学得好时，测试你的英语，你不可能保证你英语测试也能通过。
因此训练样本和测试样本要都独立同分布的来自于概率分布P。
数据窥探（的危害）。
在学习过程的任何一步中数据集都可能被影响。
假设有8年的交易数据，将前6年的作为训练数据，后2年的作为测试数据，期望得到通过前二十天的数据预测出第21天交易，通过有偷窥和没有偷窥两种预测的收益情况作对比害，如图16-2所示，红色部分为使用8年的放缩统计数据建立模型预测后两年的收益情况，蓝色部分是使用前6年的数据建立模型预测后两年的收益情况。从该图表可知即使是间接的偷窥了统计信息的模型也比完全不偷窥的模型表现好处很多。
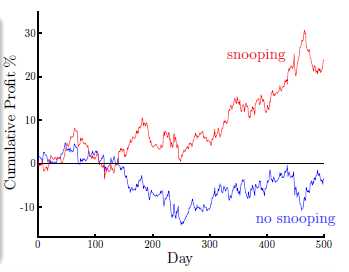
图16-2 偷窥与否的收益对比图
当然在做机器学习时很难做到不偷窥，只可能做到尽量避免，比保留验证数据做验证等。对所有的情况都存在质疑。
三的威力。
本节是对整个课程做一次总结，总结中发现此课程介绍的内容很巧的都与数字三有关，本节的题目因此得名。
首先本课程介绍了三种与机器学习有关的领域：数据挖掘、人工智能和统计。
三个理论保证：霍夫丁不等式（单一假设确认时使用）、多箱霍夫丁不等式（有限多个假设验证时使用）和VC限制（无限多个假设训练时使用）。
三个模型：二元分类模型（包含PLA和pocket）、线性回归和logistic回归。
三种重要工具：特征转换、正则化和验证。
三个原则：奥克姆剃刀、抽样偏差和数据窥探。
未来学习的方向也分为三种：更多的转换方式、更多的正则化和没有标记的情况。
原文：http://www.cnblogs.com/ymingjingr/p/5186487.html