二叉堆是一种特殊的堆,二叉堆是完全二元树(二叉树)或者是近似完全二元树(二叉树)。
二叉堆有两种:最大堆和最小堆。
最大堆:父结点的键值总是大于或等于任何一个子结点的键值;
最小堆:父结点的键值总是小于或等于任何一个子节点的键值。
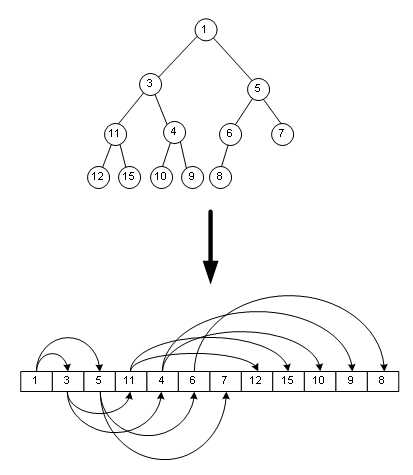
二叉堆一般都通过"数组"来实现。数组实现的二叉堆,父节点和子节点的位置存在一定的关系。我们将"二叉堆的第一个元素"放在数组索引0的位置。
假设"第一个元素"在数组中的索引为 0 的话,则父节点和子节点的位置关系如下:
1、索引为i的左孩子的索引是 (2*i+1);
2、索引为i的左孩子的索引是 (2*i+2);
3、索引为i的父结点的索引是 floor((i-1)/2);
二叉堆这种有序队列如何入队呢?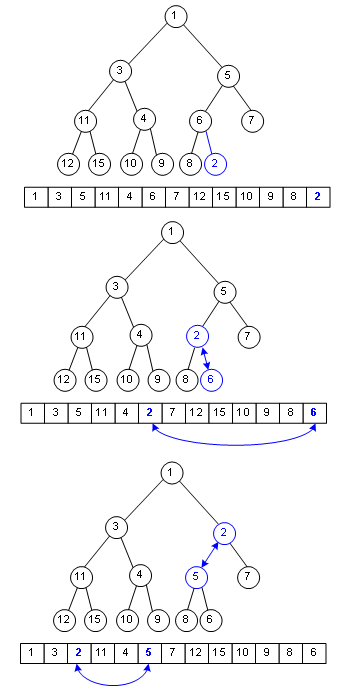
假设要在这个二叉堆里入队一个单元,只要在数组末尾加入这个元素,然后把这个元素往上挪,直到挪不动,经过了这种复杂度为Ο(logn)的操作,二叉堆性质没有变化。
那如何出队呢?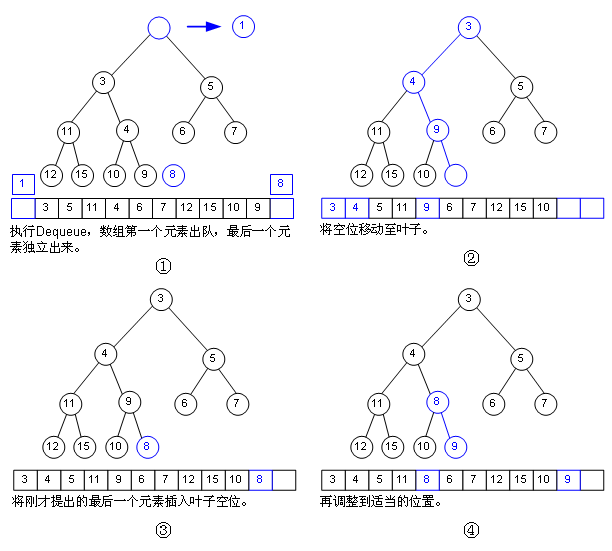
我们习惯将二叉堆画成树的形式,但本质上还是用数组实现的。
具体代码如下:
1 #include <vector> 2 #include <iostream> 3 using namespace std; 4 5 template <typename T> 6 class MinHeap 7 { 8 public: 9 vector<T> m_array; 10 int m_size;//总容量 11 private: 12 //最小堆的向下调整算法 13 void FilterDown(int start, int end); 14 //最小堆的向上调整算法 15 void FilterUp(int start); 16 public: 17 MinHeap(); 18 MinHeap(int capacity); 19 MinHeap(vector<T> data); 20 ~MinHeap(); 21 22 //返回data在vector中的索引 23 int GetIndex(T data); 24 //删除最小堆中的data 25 bool Remove(T data); 26 //将data插入到最小堆中 27 void Insert(T data); 28 //打印 29 void Print(); 30 }; 31 32 template <typename T> 33 MinHeap<T>::MinHeap(vector<T> data) 34 { 35 for (auto val : data) 36 { 37 Insert(val); 38 } 39 } 40 41 42 template <typename T> 43 MinHeap<T>::MinHeap(int capacity) 44 { 45 m_array.reserve(capacity); 46 m_capacity = capacity; 47 } 48 49 template <typename T> 50 MinHeap<T>::MinHeap() 51 { 52 m_array.reserve(100); 53 } 54 55 56 template <typename T> 57 MinHeap<T>::~MinHeap() 58 { 59 m_size = 0; 60 m_array.clear(); 61 } 62 63 //得到data的索引,-1表示未找到 64 template <typename T> 65 int MinHeap<T>::GetIndex(T data) 66 { 67 for (int i = 0; i < m_size; ++i) 68 { 69 if (m_array[i] == data) 70 return i; 71 } 72 return -1; 73 } 74 75 76 /* 77 * 最小堆的向下调整算法 78 * 79 * 数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。 80 * 81 * start -- 被下调节点的起始位置(一般为0,表示从第1个开始) 82 * end -- 截至范围(一般为数组中最后一个元素的索引) 83 */ 84 template <typename T> 85 void MinHeap<T>::FilterDown(int start, int end) 86 { 87 int current = start;//当前结点位置 88 int left = 2 * current + 1;//左儿子位置 89 T tmp = m_array[current];//当前结点大小 90 91 while (left <= end) 92 { 93 if (left < end && m_array[left] > m_array[left + 1]) 94 { 95 left++;//左右孩子选较小者 96 } 97 if (tmp <= m_array[left]) 98 break;//调整结束 99 else 100 { 101 m_array[current] = m_array[left]; 102 current = left; 103 left = 2 * left + 1; 104 } 105 } 106 m_array[current] = tmp; 107 } 108 109 //删除最小堆中的data 110 template <typename T> 111 bool MinHeap<T>::Remove(T data) 112 { 113 int index; 114 if (m_size == 0) 115 return false; 116 index = GetIndex(data); 117 if (index == -1) 118 return false; 119 m_array[index] = m_array[--m_size]; 120 m_array.erase(m_array.end() - 1); 121 FilterDown(index, m_size - 1); 122 return true; 123 } 124 125 //向上调整 126 template <typename T> 127 void MinHeap<T>::FilterUp(int start) 128 { 129 int current = start; 130 int p = (current - 1) / 2;//父结点位置 131 T tmp = m_array[current]; 132 while (current > 0) 133 { 134 if (m_array[p] <= tmp) 135 break; 136 else 137 { 138 m_array[current] = m_array[p]; 139 current = p; 140 p = (p - 1) / 2; 141 } 142 } 143 m_array[current] = tmp; 144 } 145 146 147 template <typename T> 148 void MinHeap<T>::Insert(T data) 149 { 150 m_array.push_back(data); 151 m_size++; 152 FilterUp(m_size - 1); 153 } 154 155 156 template <typename T> 157 void MinHeap<T>::Print() 158 { 159 for (auto val : m_array) 160 { 161 cout << val << " "; 162 } 163 }
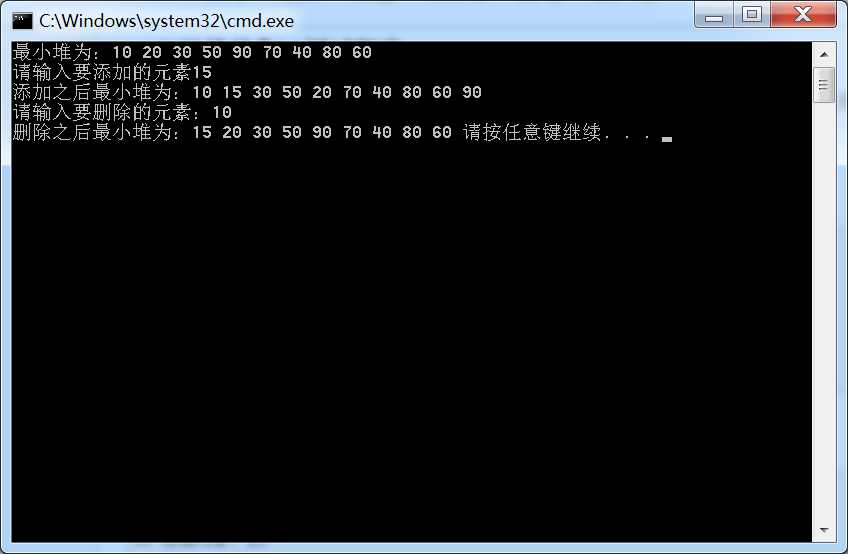
测试:
1 #include "BinaryHeap.h" 2 3 int main() 4 { 5 int tmp; 6 vector<int> vec{ 80, 40, 30, 60, 90, 70, 10, 50, 20 }; 7 MinHeap<int> heap(vec); 8 cout << "最小堆为:"; 9 heap.Print(); 10 cout << "\n请输入要添加的元素"; 11 cin >> tmp; 12 heap.Insert(tmp); 13 cout << "添加之后最小堆为:"; 14 heap.Print(); 15 cout << "\n请输入要删除的元素:"; 16 cin >> tmp; 17 heap.Remove(tmp); 18 cout << "删除之后最小堆为:"; 19 heap.Print(); 20 21 }
原文:http://www.cnblogs.com/zhangbaochong/p/5188288.html