栈:一种只能在一端进行插入和删除的特殊线性表,按照先进后出的方式组织数据,先进入的数据被压入栈底,最后的数据被压入栈顶,需要读取数据时从栈顶开始弹出数据
队列:一种只能在一端进行数据的插入及另一端进行数据的删除的特殊线性表,按照先进先出的方式组织数据
堆:N个元素{k1, k2, k3, k4, k5, k6 ... kn}组成的集合,若满足下列关系之一则可称之为堆:
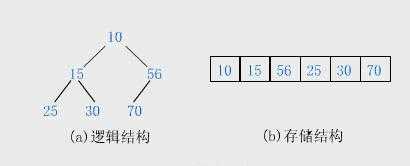
小根堆的图示如下:
栈的简单实现:
// Author: Waihui Zheng // 栈 #include <iostream> #include <assert.h> namespace my_space { template <typename T> class stack { public: stack() : _top_index(0) {} ~stack() {} void push(const T& value) { assert(_top_index < MAXN); _array[_top_index++] = value; } void pop() { assert(_top_index > 0); --_top_index; } T& top() { assert(_top_index > 0); return _array[_top_index - 1]; } const T& top() const { assert(_top_index > 0); return _array[_top_index - 1]; } bool empty() const { return _top_index == 0; } bool full() const { return _top_index == MAXN; } private: static const int MAXN = 1000; T _array[MAXN]; int _top_index; }; } int main() { my_space::stack<int> st; st.push(7); st.push(8); st.push(9); while (!st.empty()) { std::cout << st.top() << " "; st.pop(); } std::cout << std::endl; return 0; }
队列的简单实现:
// Author: Waihui Zheng // 队列 #include <iostream> #include <assert.h> namespace my_space { template <typename T> class queue { public: queue() : _front_index(0), _last_index(0) {} ~queue() {} void push(const T& value) { assert(!full()); _array[_front_index] = value; _front_index = (_front_index + 1) % MAXN; } void pop() { assert(!empty()); _last_index = (_last_index + 1) % MAXN; } T& front() { assert(!empty()); int index = _front_index - 1; if (index < 0) { index += MAXN; } return _array[index]; } const T& front() const { assert(!empty()); int index = _front_index - 1; if (index < 0) { index += MAXN; } return _array[index]; } T& back() { assert(!empty()); return _array[_last_index]; } const T& back() const { assert(!empty()); return _array[_last_index]; } bool empty() const { return _front_index == _last_index; } bool full() const { return (_front_index + 1) % MAXN == _last_index; } private: static const int MAXN = 1000; T _array[MAXN]; int _front_index; // 前方插入 int _last_index; // 后方删除 }; } int main() { my_space::queue<int> q; q.push(7); q.push(8); q.push(9); while (!q.empty()) { std::cout << q.back() << " "; q.pop(); } std::cout << std::endl; return 0; }
堆的简单实现:
// Author: Waihui Zheng // 堆 // N个元素{k1, k2, k3, k4, k5, k6 ... kn}组成的集合,若满足下列关系之一则可称之为堆 // 1. ki <= k2i 且 ki <= k2i+1, (i = 1, 2, 3 ... n/2) // 2. ki >= k2i 且 ki >= k2i+1, (i = 1, 2, 3 ... n/2) #include <iostream> #include <algorithm> #include <assert.h> namespace my_space { template <typename T> class MaxHeap { public: MaxHeap() : _length(0) {} ~MaxHeap() {} // 插入操作,则是将将元素追加于数据尾部,然后向上调堆 void push(const T& value) { // 下标从1开始,最多只能存放MAXN - 1个元素 assert(_length < MAXN - 1); _array[++_length] = value; adjust_heap_up(_array, _length); } // 堆的删除操作,则是将第一个元素删除,将最后一个元素放于第一个位置,然后向下调堆 void pop() { assert(_length > 0); std::swap(_array[1], _array[_length]); --_length; if (_length <= 0) { return ; } adjust_heap_down(_array, 1, _length); } void print() { for (int i = 1; i <= _length; ++i) { std::cout << _array[i] << " "; } std::cout << std::endl; } // 便于理解,依然元素小标从1开始 void heap_sort(T* array, int length) { for (int root = length / 2; root >= 1; --root) { adjust_heap_down(array, root, length); } for (int last_index = length; last_index > 1;) { std::swap(array[1], array[last_index]); --last_index; adjust_heap_down(array, 1, last_index); } } private: // 向下调堆,用于删除操作 void adjust_heap_down(T* data, int root_index, int last_index) { T temp = data[root_index]; int cur_index = root_index * 2; while (cur_index <= last_index) { // 选取子节点键值最大的节点 if (cur_index < last_index && data[cur_index + 1] > data[cur_index]) { ++cur_index; } // 若当前节点的键值 小于等于 父节点的键值,说明调堆成功并结束 if (data[cur_index] <= temp) { break; } // 当前节点键值大于父节点,当前键值上移 data[root_index] = data[cur_index]; root_index = cur_index; cur_index = 2 * root_index; } data[root_index] = temp; } // 向上调堆,用于插入操作,元素下标从1开始 void adjust_heap_up(T* data, int value_index) { T temp = data[value_index]; for (int cur_index = value_index / 2; cur_index >= 1; value_index = cur_index, cur_index /= 2) { if (data[cur_index] >= temp) { break; } data[value_index] = data[cur_index]; } data[value_index] = temp; } private: static const int MAXN = 1000; T _array[MAXN]; // 为便于理解,数组第一个元素从下标1开始 int _length; }; } int main() { my_space::MaxHeap<int> max_heap; int a[] = {88888, 3, 1, 5, 7, 10, 2}; max_heap.heap_sort(a, sizeof(a) / sizeof(int) - 1); for (int i = 0; i < sizeof(a) / sizeof(int); ++i) { std::cout << a[i] << " "; } std::cout << std::endl; max_heap.push(5); max_heap.push(10); max_heap.push(13); max_heap.push(4); max_heap.push(18); max_heap.print(); max_heap.pop(); max_heap.print(); return 0; }
原文:http://www.cnblogs.com/bugfly/p/5192012.html