中国剩余定理,又名孙子定理o(*≧▽≦)ツ
能求解什么问题呢?
问题:
一堆物品
3个3个分剩2个
5个5个分剩3个
7个7个分剩2个
问这个物品有多少个
解这题,我们需要构造一个答案
我们需要构造这个答案
5*7*inv(5*7, 3) % 3 = 1
3*7*inv(3*7, 5) % 5 = 1
3*5*inv(3*5, 7) % 7 = 1
这3个式子对不对,别告诉我逆元你忘了(*´∇`*),忘了的人请翻阅前几章复习
然后两边同乘你需要的数
2 * 5*7*inv(5*7, 3) % 3 = 2
3 * 3*7*inv(3*7, 5) % 5 = 3
2 * 3*5*inv(3*5, 7) % 7 = 2
令
a = 2 * 5*7*inv(5*7, 3)
b = 3 * 3*7*inv(3*7, 5)
c = 2 * 3*5*inv(3*5, 7)
那么
a % 3 = 2
b % 5 = 3
c % 7 = 2
其实答案就是a+b+c
因为
a%5 = a%7 = 0 因为a是5的倍数,也是7的倍数
b%3 = b%7 = 0 因为b是3的倍数,也是7的倍数
c%3 = c%5 = 0 因为c是3的倍数,也是5的倍数
所以
(a + b + c) % 3 = (a % 3) + (b % 3) + (c % 3) = 2 + 0 + 0 = 2
(a + b + c) % 5 = (a % 5) + (b % 5) + (c % 5) = 0 + 3 + 0 = 3
(a + b + c) % 7 = (a % 7) + (b % 7) + (c % 7) = 0 + 0 + 2 = 2
你看你看,答案是不是a+b+c(??ω?)??,完全满足题意
但是答案,不只一个,有无穷个,每105个就是一个答案(105 = 3 * 5 * 7)
根据计算,答案等于233,233%105 = 23
如果题目问你最小的那个答案,那就是23了
以下抄自百度百科
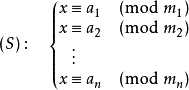
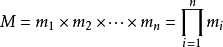
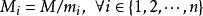
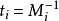
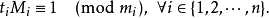
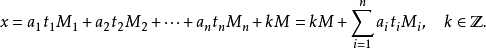
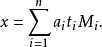
1 //n个方程:x=a[i](mod m[i]) (0<=i<n) 2 LL china(int n, LL *a, LL *m){ 3 LL M = 1, ret = 0; 4 for(int i = 0; i < n; i ++) M *= m[i]; 5 for(int i = 0; i < n; i ++){ 6 LL w = M / m[i]; 7 ret = (ret + w * inv(w, m[i]) * a[i]) % M; 8 } 9 return (ret + M) % M; 10 }
当然,这个中国剩余定理只是基础,面对更强大的敌人,我们要有更强的武器
比如,m1,m2, ... ,mn两两不保证互质,辣怎么办(っ °Д °)っ
别怕,看我接着抛代码
1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 typedef long long LL; 5 typedef pair<LL, LL> PLL; 6 PLL linear(LL A[], LL B[], LL M[], int n) {//求解A[i]x = B[i] (mod M[i]),总共n个线性方程组 7 LL x = 0, m = 1; 8 for(int i = 0; i < n; i ++) { 9 LL a = A[i] * m, b = B[i] - A[i]*x, d = gcd(M[i], a); 10 if(b % d != 0) return PLL(0, -1);//答案,不存在,返回-1 11 LL t = b/d * inv(a/d, M[i]/d)%(M[i]/d); 12 x = x + m*t; 13 m *= M[i]/d; 14 } 15 x = (x % m + m ) % m; 16 return PLL(x, m);//返回的x就是答案,m是最后的lcm值 17 }
这个代码我不给予解释(因为我不会,哇哈哈哈╰(*°▽°*)╯)
遇到需要的题就去套模板吧
比如poj 2891
http://poj.org/problem?id=2891
【题目大意】
给出k个模方程组:x mod ai = ri。求x的最小正值。如果不存在这样的x,那么输出-1.
【题目分析】
由于这道题目里面的ai、ri之间不满足两两互质的性质,所以不能用中国剩余定理直接求解。
辣么。。。。愉快的套这个模板吧
AC代码如下:

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 typedef long long LL; 5 typedef pair<LL, LL> PLL; 6 LL a[100000], b[100000], m[100000]; 7 LL gcd(LL a, LL b){ 8 return b ? gcd(b, a%b) : a; 9 } 10 void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){ 11 if (!b) {d = a, x = 1, y = 0;} 12 else{ 13 ex_gcd(b, a % b, y, x, d); 14 y -= x * (a / b); 15 } 16 } 17 LL inv(LL t, LL p){//如果不存在,返回-1 18 LL d, x, y; 19 ex_gcd(t, p, x, y, d); 20 return d == 1 ? (x % p + p) % p : -1; 21 } 22 PLL linear(LL A[], LL B[], LL M[], int n) {//求解A[i]x = B[i] (mod M[i]),总共n个线性方程组 23 LL x = 0, m = 1; 24 for(int i = 0; i < n; i ++) { 25 LL a = A[i] * m, b = B[i] - A[i]*x, d = gcd(M[i], a); 26 if(b % d != 0) return PLL(0, -1);//答案,不存在,返回-1 27 LL t = b/d * inv(a/d, M[i]/d)%(M[i]/d); 28 x = x + m*t; 29 m *= M[i]/d; 30 } 31 x = (x % m + m ) % m; 32 return PLL(x, m);//返回的x就是答案,m是最后的lcm值 33 } 34 int main(){ 35 int n; 36 while(scanf("%d", &n) != EOF){ 37 for(int i = 0; i < n; i ++){ 38 a[i] = 1; 39 scanf("%d%d", &m[i], &b[i]); 40 } 41 PLL ans = linear(a, b, m, n); 42 if(ans.second == -1) printf("-1\n"); 43 else printf("%I64d\n", ans.first); 44 } 45 }
你看,全是我的模板,套来套去
哇哈哈哈╰(*°▽°*)╯
哇哈哈哈╰(*°▽°*)╯
哇哈哈哈╰(*°▽°*)╯
哇哈哈哈╰(*°▽°*)╯
哇哈哈哈╰(*°▽°*)╯
哇哈哈哈╰(*°▽°*)╯
ACM数论之旅9---中国剩余定理(壮哉我大中华╰(*°▽°*)╯)
原文:http://www.cnblogs.com/linyujun/p/5199415.html