Note of Markov Chain Monte Carlo and Gibbs Sampling : http://pan.baidu.com/s/1jHpWY1o
序:A major limitation towards more widespread implementation of Bayesian approaches is that obtaining thee posterior distribution often requires the integration of high-dimensional functions. Here the MCMC is used to solve this problem. There are two major method in the using of MCMC ---- Metropolis algorithm and Gibbs sampling.
问题:计算一个复杂积分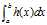
解决方案:把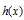 分解成
分解成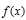 和
和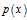 ,要求
,要求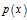 是概率密度函数,得到
是概率密度函数,得到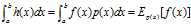 ,将函数积分转换为随机变量函数的期望进行计算。
,将函数积分转换为随机变量函数的期望进行计算。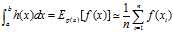 ,这里的xi是服从概率分布密度为
,这里的xi是服从概率分布密度为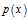 的随机变量x的取值。
的随机变量x的取值。
应用在贝叶斯理论中,后验概率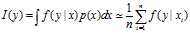 。
。
介绍了马尔科夫过程,马尔可夫链,状态空间,转移概率,转移矩阵,以及切普曼-柯尔莫哥洛夫方程,平稳分布等概念。这里提及了从离散的平稳分布向连续状态进行过渡: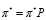 à
à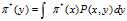
问题:从复杂的概率分布p(x)中采样。
解决方案:假如我们要从p(x)=f(x)/K中采样,但是K 并不已知且无法求取,则采取如下方法进行采样
a.设定初始值x0,要满足f(x0)>0;
b.利用现在的x值,从转移分布q(x1,x2)中采样一个候选参数x*,对这个转移分布的限制是q(x1,x2)=q(x2,x1);
c.计算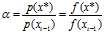 (这里用的是比值所以可以避开K 进行计算);
(这里用的是比值所以可以避开K 进行计算);
d.如果alpha大于1则接受候选 x*;如果alpha小于1,则以概率alpha接受候选x*;然后返回到步骤b.
4. The Gibbs Sampler
这种采样方法应用在多变量的分布当中,在采样时,我们每次只对一个变量进行采样将其他变量固定。也就是说每次都是对一个单变量的条件分布进行采样,而不去理会联合分布,这样对n个变量进行轮流采样,进行k轮之后得到一个长度为k 的Gibbs Sequence 用来表示联合分布的采样。文章中的Example 4里列出了一个二维的联合分布的采样过程,他的两个条件分布分别为二项分布和Beta分布,很好的诠释 了Gibbs采样的流程和优势。
另外,这里还比较了吉布斯采样和EM算法的联系与区别。
EM每次都包含两个步骤:a.在固定参数下对隐变量求期望;b.固定隐变量的取值,利用极大似然的方法对参数数进行估计。
吉布斯采样则将隐变量和参数看成同等地位进行随机采样,可以看成是对EM算法的随机模拟。(原文:The Gibbs sampler can be thought of as a stochastic analog to the EM approaches used to obtain likelihood functions when missing data are present .)
参考:《统计学习方法》;
《Pattern recognition and machine learning 》第十一章 .
原文:http://www.cnblogs.com/simayuhe/p/5199809.html