二叉搜索树,亦称二叉查找树,二叉排序树,它满足以下性质:
二叉搜索树的遍历:
例子:
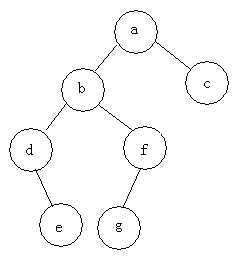
先序遍历:abdefgc
中序遍历:debgfac
后序遍历:edgfbca
二叉搜索树的删除操作:
二叉树删除操作主要分三种情况:
简单示例代码如下:
// Author: Waihui Zheng // binary search tree #include <iostream> #include <algorithm> #include <queue> #include <stack> namespace my_space { template <typename T> class BinarySearchTree { struct TreeNode { T value; TreeNode* left; TreeNode* right; TreeNode() : value(), left(NULL), right(NULL) {} TreeNode(const T& v) : value(v), left(NULL), right(NULL) {} }; public: BinarySearchTree() : _root(NULL) {} ~BinarySearchTree() { free_nodes(_root); _root = NULL; } // 递归方式调用 void insert_recursive(const T& value) { insert_recursive(_root, value); } bool search_recursive(const T& value) { return search_recursive(_root, value); } void delete_recursive(const T& value) { delete_recursive(_root, value); } void inorder_recursive() { std::cout << "递归中序: "; inorder_recursive(_root); std::cout << std::endl; } void preorder_recursive() { std::cout << "递归先序: "; preorder_recursive(_root); std::cout << std::endl; } void postorder_recursive() { std::cout << "递归后序: "; postorder_recursive(_root); std::cout << std::endl; } // 非递归方式调用 void insert_nonrecursive(const T& value) { insert_nonrecursive(_root, value); } bool search_nonrecursive(const T& value) { return search_nonrecursive(_root, value); } void delete_nonrecursive(const T& value) { delete_nonrecursive(_root, value); } void preorder_nonrecursive() { std::cout << "非递归先序: "; preorder_nonrecursive(_root); std::cout << std::endl; } void inorder_nonrecursive() { std::cout << "非递归中序: "; inorder_nonrecursive(_root); std::cout << std::endl; } void postorder_nonrecursive() { std::cout << "非递归后序: "; postorder_nonrecursive(_root); std::cout << std::endl; } void clear() { free_nodes(_root); _root = NULL; } private: // 使用后序遍历,对树节点进行回收内存 void free_nodes(TreeNode* root) { if (NULL == root) { return ; } free_nodes(root->left); free_nodes(root->right); delete root; } // 递归方式 // 递归插入节点到相应位置,利用引用,可以直接知道节点被插入的具体位置 void insert_recursive(TreeNode*& root, const T& value) { if (NULL == root) { root = new TreeNode(value); } if (root->value == value) { return ; } value < root->value ? insert_recursive(root->left, value) : insert_recursive(root->right, value); } bool search_recursive(TreeNode* root, const T& value) { if (root == NULL) { return false; } if (root->value == value) { return true; } if (value < root->value) { return search_recursive(root->left, value); } else { return search_recursive(root->right, value); } } void delete_recursive(TreeNode*& root, const T& value) { if (root == NULL) { return ; } if (value < root->value) { // 往左边寻找 delete_recursive(root->left, value); } else if (value > root->value) { // 往右边寻找 delete_recursive(root->right, value); } else { //发现value的节点 if (root->left == NULL && root->right == NULL) { // 目标节点为叶节点 delete root; root = NULL; // root为引用,可以知道目标节点被谁所指 } else if (root->left == NULL) { // 目标节点只有右子树 TreeNode* p = root; root = root->right; delete p; } else if (root->right == NULL) { // 目标节点只有左子树 TreeNode* p = root; root = root->left; delete p; } else { // 目标节点左右子树均存在 TreeNode* parent = root; TreeNode* cur = root->left; while (cur->right != NULL) { // 寻找左子树的最大值,cur指向的节点为左子树的最大值节点,且没有右子树 parent = cur; cur = cur->right; } root->value = cur->value; // 左子树最大值赋给目标节点 parent == root ? // 两种情况,左子树根节点没有右孩子 及 左子树根节点有右孩子 parent->left = cur->left : parent->right = cur->left; delete cur; } } } // 根->左子树->右子树 void preorder_recursive(TreeNode* root) { if (root == NULL) { return ; } std::cout << root->value << " "; preorder_recursive(root->left); preorder_recursive(root->right); } // 左子树->根->右子树 void inorder_recursive(TreeNode* root) { if (root == NULL) { return ; } inorder_recursive(root->left); std::cout << root->value << " "; inorder_recursive(root->right); } // 左子树->右子树->根 void postorder_recursive(TreeNode* root) { if (root == NULL) { return ; } postorder_recursive(root->left); postorder_recursive(root->right); std::cout << root->value << " "; } // 非递归方式调用 void insert_nonrecursive(TreeNode* root, const T& value) { if (root == NULL) { _root = new TreeNode(value); return ; } TreeNode* cur = root; while (cur != NULL) { if (value == cur->value) { return ; } if (value < cur->value) { // 往左子树寻找 if (cur->left != NULL) { // 若左子树存在,继续左移 cur = cur->left; } else { // 若左子树不存在,那么直接插入新节点 cur->left = new TreeNode(value); return ; } } else { // 往右子树寻找 if (cur->right != NULL) { // 若右子树存在,继续右移 cur = cur->right; } else { // 若右子树不存在,那么直接插入新节点 cur->right = new TreeNode(value); return ; } } } } bool search_nonrecursive(TreeNode* root, const T& value) { if (root == NULL) { return false; } TreeNode* cur = root; while (cur != NULL) { if (cur->value == value) { return true; } cur = value < cur->value ? cur->left : cur->right; } return false; } void delete_nonrecursive(TreeNode* root, const T& value) { if (root == NULL) { return ; } TreeNode* pre = NULL; // 需要记录目标节点的父节点 TreeNode* cur = root; // cur将指向目标节点 while (cur != NULL) { if (value == cur->value) { // 找到目标节点 if (cur->left == NULL && cur->right == NULL) { // 目标节点为叶节点 if (pre == NULL) { // 说明当前节点是根节点 delete cur; _root = NULL; } else { // 先判断目标节点是左孩子还是右孩子 pre->left == cur ? pre->left = NULL : pre->right = NULL; delete cur; } } else if (cur->left != NULL && cur->right == NULL) { // 目标节点只有左子树 if (pre == NULL) { // 说明当前节点是根节点 _root = cur->left; delete cur; } else { // 先判断目标节点是左孩子还是右孩子 pre->left == cur ? pre->left = cur->left : pre->right = cur->left; delete cur; } } else if (cur->left == NULL && cur->right != NULL) { // 目标节点只有右子树 if (pre == NULL) { // 说明当前节点是根节点 _root = cur->right; delete cur; } else { // 先判断目标节点是左孩子还是右孩子 pre->left == cur ? pre->left = cur->right : pre->right = cur->right; delete cur; } } else { // 目标节点左右子树均存在 TreeNode* extra_pre = cur; // extra_cur指向节点的父节点 TreeNode* extra_cur = cur->left; // 将指向目标节点 左子树的最大值 while (extra_cur->right != NULL) { // 寻找左子树的最大值 extra_pre = extra_cur; extra_cur = extra_cur->right; } cur->value = extra_cur->value; if (cur == extra_pre) { // 若 目标节点的左子树根节点没有右孩子 cur->left = extra_cur->left; } else { extra_pre->right = extra_cur->left; } delete extra_cur; } return ; } if (value < cur->value) { // 往左子树寻找 pre = cur; cur = cur->left; } else { // 往右子树寻找 pre = cur; cur = cur->right; } } } void preorder_nonrecursive(TreeNode* root) { if (root == NULL) { return ; } std::stack<TreeNode*> st; st.push(root); while (!st.empty()) { TreeNode* cur = st.top(); st.pop(); std::cout << cur->value << " "; if (cur->right != NULL) { // 右孩子不为空,则先放右孩子 st.push(cur->right); } if (cur->left != NULL) { // 左孩子不为空,则放左孩子 st.push(cur->left); } } } void inorder_nonrecursive(TreeNode* root) { if (root == NULL) { return ; } std::stack<TreeNode*> st; TreeNode* cur = root; while (cur != NULL) { // 优先将左孩子依次放入栈中 st.push(cur); cur = cur->left; } while (!st.empty()) { cur = st.top(); st.pop(); std::cout << cur->value << " "; cur = cur->right; while (cur != NULL) { // 优先将左孩子依次放入栈中 st.push(cur); cur = cur->left; } } } void postorder_nonrecursive(TreeNode* root) { if (root == NULL) { return ; } std::stack<TreeNode*> st; TreeNode* pre = NULL; st.push(root); while (!st.empty()) { TreeNode* cur = st.top(); // 若当前节点为叶节点,则访问 // 若当前节点的前驱等于当前节点的左孩子或右孩子,则访问 if ((cur->left == NULL && cur->right == NULL) || (pre != NULL && (pre == cur->left || pre == cur->right))) { std::cout << cur->value << " "; pre = cur; st.pop(); } else { if (cur->right != NULL) { // 右孩子不为空,则先放右孩子 st.push(cur->right); } if (cur->left != NULL) { // 左孩子不为空,则放左孩子 st.push(cur->left); } } } } private: TreeNode* _root; }; } void show_recursive() { std::cout << "递归方式" << std::endl; my_space::BinarySearchTree<int> btree; btree.insert_recursive(7); btree.insert_recursive(1); btree.insert_recursive(3); btree.insert_recursive(10); btree.insert_recursive(2); btree.insert_recursive(9); btree.insert_recursive(4); btree.preorder_recursive(); btree.inorder_recursive(); btree.postorder_recursive(); std::cout << "5 " << (btree.search_recursive(5) ? "存在" : "不存在") << std::endl; std::cout << "10 " << (btree.search_recursive(10) ? "存在" : "不存在") << std::endl; btree.delete_recursive(7); btree.inorder_recursive(); std::cout << std::endl; btree.delete_recursive(3); btree.inorder_recursive(); std::cout << std::endl; std::cout << std::endl; } void show_nonrecursive() { std::cout << "非递归方式" << std::endl; my_space::BinarySearchTree<int> btree; btree.insert_nonrecursive(7); btree.insert_nonrecursive(1); btree.insert_nonrecursive(3); btree.insert_nonrecursive(10); btree.insert_nonrecursive(2); btree.insert_nonrecursive(9); btree.insert_nonrecursive(4); btree.preorder_nonrecursive(); btree.inorder_nonrecursive(); btree.postorder_nonrecursive(); std::cout << "5 " << (btree.search_nonrecursive(5) ? "存在" : "不存在") << std::endl; std::cout << "10 " << (btree.search_nonrecursive(10) ? "存在" : "不存在") << std::endl; btree.delete_nonrecursive(7); btree.inorder_recursive(); std::cout << std::endl; btree.delete_nonrecursive(3); btree.inorder_recursive(); std::cout << std::endl; std::cout << std::endl; } int main() { show_recursive(); show_nonrecursive(); return 0; }
原文:http://www.cnblogs.com/bugfly/p/5199477.html