=== 1. and运算 ===
and运算通常用于二进制取
位操作,例如一个数 and 1的结果就是取
二进制的最末位。这可以用来判断一个整数的奇偶,二进制的最末位为0表示该数为
偶数,最末位为1表示该数为奇数。
相同位的两个数字都为1,则为1;若有一个不为1,则为0。
00101
11100
(&;或者and)
----------------
00100
=== 2. or运算 ===
or运算通常用于二进制特定位上的无条件
赋值,例如一个数or 1的结果就是把二进制最末位强行变成1。如果需要把二进制最末位变成0,对这个数or 1之后再减一就可以了,其实际意义就是把这个数强行变成最接近的偶数。
相同位只要一个为1即为1。
00101
11100
(|或者or)
----------------
11101
=== 3. xor运算 ===
异或的符号是^。按位异或运算, 对等长二进制模式按位或二进制数的每一位执行逻辑按位异或操作. 操作的结果是如果某位不同则该位为1, 否则该位为0.
xor运算的逆运算是它本身,也就是说两次异或同一个数最后结果不变,即(a xor b) xor b = a。xor运算可以用于简单的加密,比如我想对我MM说1314520,但怕别人知道,于是双方约定拿我的生日19880516作为
密钥。1314520 xor 19880516 = 20665500,我就把20665500告诉MM。MM再次计算20665500 xor 19880516的值,得到1314520,于是她就明白了我的企图。
相同位不同则为1,相同则为0。
00101
11100
(^或者xor)
----------------
11001
关键来说说这个 ~ 按位取反
要点:二进制数在内存中是以补码形式存放的。
基础:
正数
原码、补码、反码都是其本身
3的原码 0000 0011
3的反码 0000 0011
3的补码 0000 0011
负数
-3的原码 是 1000 0011 (前面4个1表示符号位)
-3的反码 是 1111 1100 (符号位不变 各位取反)
-3的补码 是 1111 1101 (符号位不变 末尾+1 注意这里是反码的基础上+1)
所以-3在内存中存储为 1111 1101
原码到补码
原码->取反->+1->补码
补码到原码
补码->-1->取反->原码
~3等于多少呢?
3的补码为 0000 0011, 按位取反 1000 1100 (符号位也要取反哦,这里并不是结果,我们需要算出原码)
补码转原码
1000 1100 先-1得 1000 1011
1000 1011 取反得 1000 0100 (这里就是~3的结果-4)
最后总结一个规律:
1. 所有正整数的按位取反是其本身+1的负数
2. 所有负整数的按位取反是其本身+1的绝对值
3. 零的按位取反是 -1(0在数学界既不是正数也不是负数)
左移右移 << >>
有了上面的原码和补码的换算基础,下面就好弄了。
左移说明:在数字没有溢出的前提下,对于正数和负数,左移一位都相当于乘以2的1次方,左移n位就相当于乘以2的n次方
按二进制形式把所有的数字向左移动对应的位数,高位移出(舍弃),低位的空位补零。
因为正数原码和补码相同,所以可以直接移动,负数要换算成补码移动,再转换成原码。
正数左移
2 << 2 :0000 0010 左移2得 0000 1000 十进制数8
负数左移(原码和补码左移位都是相同的?)
-2 << 2 :1000 0010 左移2得 1000 1000 十进制数-8
右移说明:右移一位相当于除2,右移n位相当于除以2的n次方。
按二进制形式把所有的数字向右移动对应的位数,低位移出(舍弃),高位的空位补符号位,即正数补零,负数补1,右移的规则只记住一点,符号位不变,左边补上符号位
正数右移
2 >> 2 :0000 0010 右移2得 0000 0000 十进制数0
负数右移
-2 >> 2 :1000 0010 右移2得 1000 1100 十进制数-1
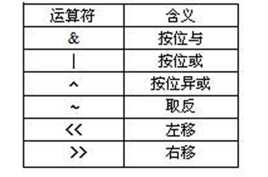
位运算 &|^~<<>>
原文:http://www.cnblogs.com/fanqiechaodan/p/5210840.html
