随着新版百度空间的上线,Blog宠物绿豆蛙完成了它的使命,去寻找它新的归宿。
给出一个有向无环图,起点为1终点为N,每条边都有一个长度,并且从起点出发能够到达所有的点,所有的点也都能够到达终点。绿豆蛙从起点出发,走向终点。
到达每一个顶点时,如果有K条离开该点的道路,绿豆蛙可以选择任意一条道路离开该点,并且走向每条路的概率为 1/K 。
现在绿豆蛙想知道,从起点走到终点的所经过的路径总长度期望是多少?
第一行: 两个整数 N M,代表图中有N个点、M条边
第二行到第 1+M 行: 每行3个整数 a b c,代表从a到b有一条长度为c的有向边
从起点到终点路径总长度的期望值,四舍五入保留两位小数。
4 4
1 2 1
1 3 2
2 3 3
3 4 4
7.00
对于20%的数据 N<=100
对于40%的数据 N<=1000
对于60%的数据 N<=10000
对于100%的数据 N<=100000,M<=2*N
Nescafe 19
期望值:在概率论和统计学中,一个离散性随机变量的期望值(或数学期望、或均值,亦简称期望,物理学中称为期待值)是试验中每次可能结果的概率乘以其结果的总和。换句话说,期望值是随机试验在同样的机会下重复多次的结果计算出的等同“期望”的平均值。需要注意的是,期望值并不一定等同于常识中的“期望”——“期望值”也许与每一个结果都不相等。(换句话说,期望值是该变量输出值的平均数。期望值并不一定包含于变量的输出值集合里。)
解释一下样例
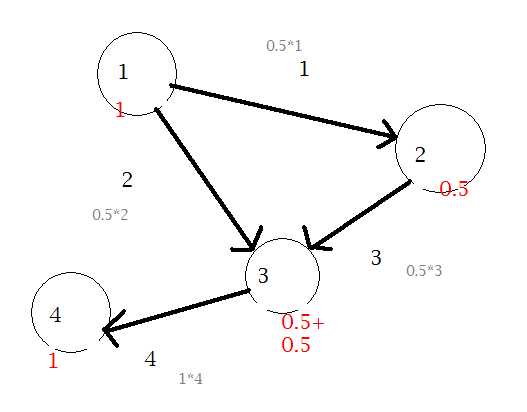 红色是点权,灰色是累加的ans
红色是点权,灰色是累加的ans
注意数据范围,边表+队列实现。
每个点都有一个权值,起点为1,然后当这个点离开拓扑序列时,把权值分解,均分给它指向的点,同时将这个权值乘上边权累加。
#include<iostream> #include<cstdio> using namespace std; const int MAXN = 100010; const int MAXM = 200010; struct node { int to,next,w; }e[MAXM]; int head[MAXN]; double pw[MAXN] = {0}; //点权 int rudu[MAXN] = {0}; int chudu[MAXN] = {0}; int q[MAXN] = {0}; //队列,放出度为0的点 int n,m,cnt= 0,u,v,w,h,t; double ans=0; void ins(int u,int v,int w) { e[++cnt].to = v; e[cnt].w = w; e[cnt].next = head[u]; head[u] = cnt; } int main() { scanf("%d%d",&n,&m); for (int i=1;i<=m;i++) { scanf("%d%d%d",&u,&v,&w); ins(u,v,w); chudu[u] ++; rudu[v] ++; } pw[1] = 1; h = 0; t = 1; q[t] = 1; while (h<t) { int j = q[++h]; double wj = pw[j]*1.0/chudu[j]; for (int k = head[j]; k; k=e[k].next) { ans += wj*e[k].w; pw[e[k].to] += wj; rudu[e[k].to] --; if (!rudu[e[k].to]) q[++t] = e[k].to; } rudu[j] = 100; } printf("%.2lf",ans); return 0; }
原文:http://www.cnblogs.com/liumengyue/p/5211709.html