堆排序中,最初的步骤就是建立一个堆。之前在一些公司的笔试题上面见到一些与建堆过程相关的题目,因为当时对建堆过程有个误解,所以经常选错。之前一直以为是在完全二叉树中依次插入序列中的元素,每插入一个元素,就调用siftup操作;而实际的建堆操作是序列中元素首先就全部填入一个完全二叉树,然后从第一个非终端节点开始,调用siftdown操作,依次调整。
堆排序过程
堆分为大根堆和小根堆,是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值,即A[PARENT[i]] >= A[i]。在数组的非降序排序中,需要使用的就是大根堆,因为根据大根堆的要求可知,最大的值一定在堆顶。
既然是堆排序,自然需要先建立一个堆,而建堆的核心内容是调整堆,使二叉树满足堆的定义(每个节点的值都不大于其父节点的值)。调堆的过程应该从最后一个非叶子节点开始,假设有数组A = {1, 3, 4, 5, 7, 2, 6, 8, 0}。那么调堆的过程如下图,数组下标从0开始,A[3] = 5开始。分别与左孩子和右孩子比较大小,如果A[3]最大,则不用调整,否则和孩子中的值最大的一个交换位置,在图1中是A[7] > A[3] > A[8],所以A[3]与A[7]对换,从图1.1转到图1.2。
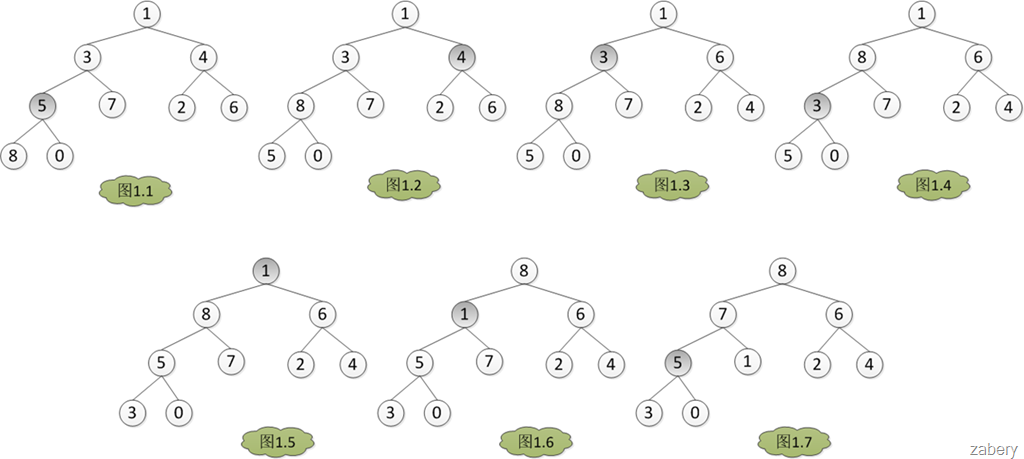
以上便是建堆的完整过程,主要总结有以下几点需要注意:
1.首先将所有元素按照初始顺序填充到一个完全二叉树中
2.从“最后一个非终端节点”开始,调用siftdown方法,调整堆的结构,直到根节点为止
堆排序的关键是要实现siftup和siftdown。当建立完这两个函数以后,排序一个数组只需要5行代码。算法执行了n-1次siftup和siftdown,而每次操作的成本最多O(lgn),所以运行时间为O(nlogn)。
-
#include <stdio.h>
-
#include <stdlib.h>
-
-
-
#define MAX 20
-
-
-
void swap( int *data, int i, int j)
-
{
-
int temp = data[i];
-
data[i] = data[j];
-
data[j] = temp;
-
}
-
-
-
-
void siftup(int *data, int n )
-
{
-
int i = n;
-
int p;
-
while( 1 )
-
{
-
if ( i == 1 ) break;
-
p = i/2;
-
if( data[p] <= data[i]) break;
-
swap( data, i, p );
-
i = p;
-
}
-
}
-
-
-
-
void siftdown( int *data, int n)
-
{
-
int i = 1;
-
int c = 0;
-
while( 1 )
-
{
-
c = 2 * i;
-
if( c > n ) break;
-
-
if( c + 1 <= n && data[ c + 1] < data[c] )
-
c++;
-
-
-
-
if( data[i] <= data[c] )
-
break;
-
swap( data, c, i);
-
i = c;
-
}
-
}
-
-
-
int main()
-
{
-
int data[ MAX + 1];
-
int i= 0;
-
srand(5);
-
for( i = 1; i <= MAX; i++ )
-
data[i] = rand() % 500;
-
-
-
-
for( i = 2; i <= MAX; i++ )
-
siftup(data,i);
-
-
-
-
for( i =MAX; i >= 2; i--)
-
{
-
swap(data, 1, i);
-
siftdown(data, i - 1 );
-
}
-
-
-
for( i = 1; i < MAX; i++ )
-
printf("%d\t", data[i]);
-
-
-
printf("\n");
-
return 0;
-
}
堆排序与系统排序的效率比较:
-
#include <stdio.h>
-
#include<iostream>
-
#include<string.h>
-
#include <algorithm>
-
#include <stdlib.h>
-
using namespace std;
-
-
#define MAX 200000
-
-
void swap( int *data, int i, int j)
-
{
-
int temp = data[i];
-
data[i] = data[j];
-
data[j] = temp;
-
}
-
-
-
void siftup(int *data, int n )
-
{
-
int i = n;
-
int p;
-
while( 1 )
-
{
-
if ( i == 1 ) break;
-
p = i/2;
-
if( data[p] <= data[i]) break;
-
swap( data, i, p );
-
i = p;
-
}
-
}
-
-
-
void siftdown( int *data, int n)
-
{
-
int i = 1;
-
int c = 0;
-
while( 1 )
-
{
-
c = 2 * i;
-
if( c > n ) break;
-
-
if( c + 1 <= n && data[ c + 1] < data[c] )
-
c++;
-
-
-
if( data[i] <= data[c] )
-
break;
-
swap( data, c, i);
-
i = c;
-
}
-
}
-
-
int main()
-
{
-
double BegTime, EndTime;
-
int data[ MAX + 1];
-
int data2[ MAX + 1];
-
data2[0] = 0;
-
int i= 0;
-
srand(5);
-
for( i = 1; i <= MAX; i++ )
-
data[i] = rand() % 500;
-
-
memcpy( data2, data, MAX+1);
-
BegTime = clock();
-
-
for( i = 2; i <= MAX; i++ )
-
siftup(data,i);
-
-
-
for( i =MAX; i >= 2; i--)
-
{
-
swap(data, 1, i);
-
siftdown(data, i - 1 );
-
}
-
EndTime = clock();
-
printf("HeapSort:%gms\n", (EndTime - BegTime) / 1000);
-
-
BegTime = clock();
-
sort(data2, data2 + MAX + 1);
-
EndTime = clock();
-
printf("sort: %gms\n", (EndTime - BegTime) / 1000);
-
-
-
printf("\n");
-
return 0;
-
}
测试结果如下:
HeapSort:60ms
sort: 40ms
结果表明,堆排序确实有着相当不错的表现,不到必须的时候,还是应当使用系统的sort函数,效率很高,且节约开发成本。
堆排序,布布扣,bubuko.com
堆排序
原文:http://blog.csdn.net/as365927660/article/details/24146859
