(我和lesphere,reverse研究了这个东西一上午)QAQ
kmp是求字符串S的任意前缀与字符串T的最长的相同的前缀和后缀
exkmp第求字符串S的任意后缀与字符串T的最长公共前缀
与kmp相同,我们先来看S与S自己匹配,也就是求S得任意后缀与S的最长公共前缀pre[]数组
假设我们已经得到了k之前的所有答案:pre[0~k-1] 和 k之前使得i+pre[i]最大的点a(也就是能够延伸到最远的点)
如果a+pre[a]-1(延伸最远的位置)<k(不包含k)那么就暴力往后找就对了
如图是当a+pre[a]-1能包含k的情况:

显然s[0~pre[a]-1]==s[a~a+pre[a]-1]两个矩形是完全相同的(并且s[pre[a]+1]!=s[a+pre[a]]);
而且k在前面矩形中对应点k-a
那么现在有三种情况:
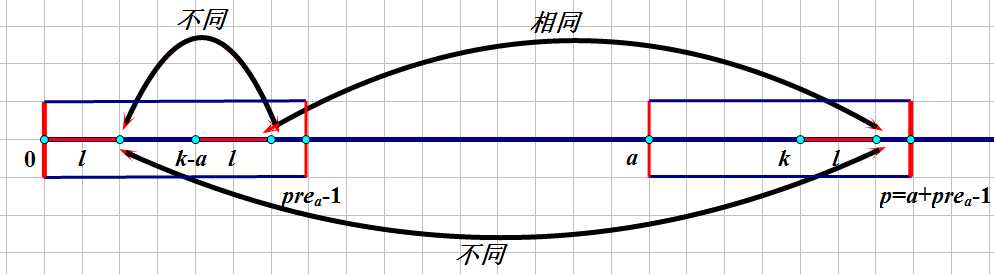
(1):pre[k-a]+k-a-1<pre[a]-1;
也就是说k-a延伸出去也不会超过pre[a]-1的矩形右边界假设l=pre[k-a];
换句话说就是s[l]!=s[k-a+l];
又因为两个矩形完全相同,所以pre[k]不会再在s[k+l]之后匹配上(延伸),所以pre[k]=l=pre[k-a];直接赋值就好;
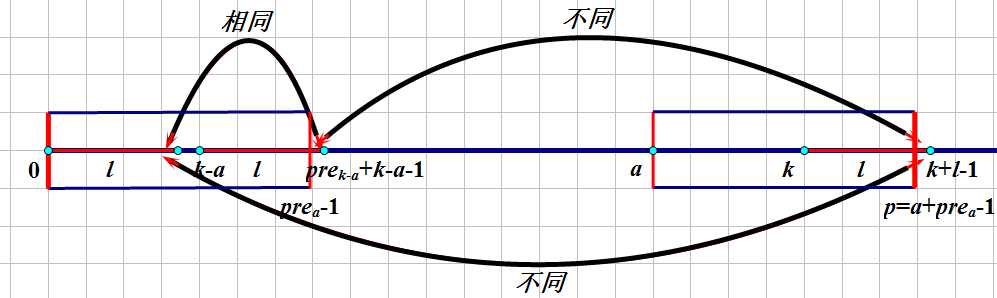
(2):pre[k-a]+k-a-1>pre[a]-1;
与情况1相反,l=pre[k-a]延伸出了矩形右边框:
如图,两个矩形右边框的右边的那个点不同(s[pre[a]+1]!=s[a+pre[a]]);
又因为左边两个l完全相同,所以s[pre[a]+1]==s[pre[a]-(k-a)](图中左边上面箭头(标有相同))
所以右边矩形后面第一个点s[p+1]!=s[pre[a]-(k-a)],所以pre[k]必定等于l在矩形中的部分长度,所以直接赋值就好;
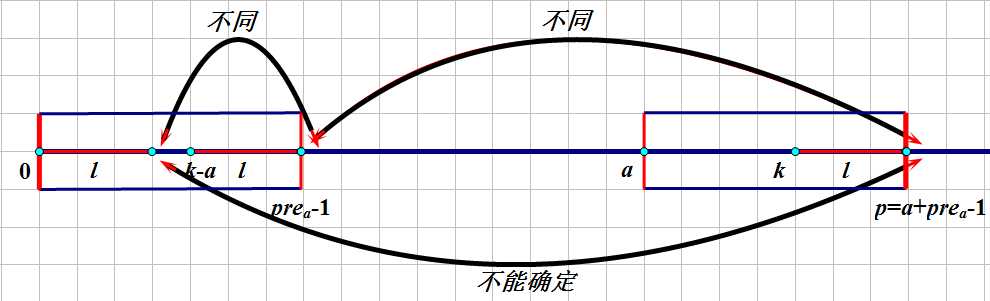
(3):pre[k-a]+k-a-1==pre[a]-1;
也就是说pre[k-a]刚好等于左边矩形右边框;
如图,由于s[pre[i]+i]!=s[pre[i]]的限制,导致两个不同,而下面的箭头就不能确定了;
于是我们对于这样的情况,就只有从右矩形边框暴力往后找了;
这样所有情况就讨论完了,递推即可
下面给出代码:
1 void getpre(char *s) 2 { 3 int len=strlen(s),a=0; 4 pre[0]=len; 5 while(a<len-1&&s[a]==s[a+1])a++; 6 pre[1]=a; 7 a=1; 8 re(k,2,len-1) 9 { 10 int p=a+pre[a]-1,l=pre[k-a]; 11 if(k-1+l>=p)//融合了k>p,情况(2),(3) (想一想为什么) 12 { 13 int j=(p-k+1)>0?(p-k+1):0; 14 while(k+j<len&&s[k+j]==s[j])j++; 15 pre[k]=j; 16 a=k; 17 } 18 else pre[k]=l; 19 next[k]=a; 20 } 21 }
S与自身的匹配和S与T的匹配类似,下面给出代码:
1 void extend(char *s,char *t) 2 { 3 int n=strlen(s),m=strlen(t); 4 getpre(s); 5 int p=0; 6 while(p<n&&s[p]==t[p]); 7 Max[0]=p; 8 int a=0,l; 9 re(k,1,n-1) 10 { 11 p=a+Max[a]-1;l=pre[k-a]; 12 if(k+l-1>=p) 13 { 14 int j=(p-k+1)>0?(p-k+1):0; 15 while(k+j<m&&s[k+j]==t[j])j++; 16 Max[k]=j;a=k; 17 } 18 else Max[k]=l; 19 } 20 }
是不是感觉差不多……
附上lesphere%%%代码:
1 void getfail(){ 2 fail[0]=m; 3 while(fail[1]<n && a[fail[1]]==a[fail[1]+1]) fail[1]++; 4 for(int i=2,j=1,mx=1+fail[1];i<n;i++){ 5 if(mx-1<i || mx-i==fail[i-j]){ 6 fail[i]=fail[i-j]; 7 while(fail[i]<n && a[fail[i]]==a[fail[i]+i]) fail[i]++; 8 } 9 else fail[i]=min(mx-i,fail[i-j]); 10 if(mx<i+fail[i]) j=i,mx=i+fail[i]; 11 } 12 } 13 void getex(){ 14 getfail(); 15 while(ex[0]<n && a[ex[0]]==b[ex[0]]) ex[0]++; 16 for(int i=1,j=0,mx=ex[0];i<n;i++){ 17 if(mx-1<i || mx-i==fail[i-j]){ 18 ex[i]=fail[i-j]; 19 while(ex[i]<n && a[ex[i]]==b[ex[i]+i]) ex[i]++; 20 } 21 else ex[i]=min(mx-i,fail[i-j]); 22 if(mx<i+ex[i]) j=i,mx=i+ex[i]; 23 } 24 }
原文:http://www.cnblogs.com/HugeGun/p/5215301.html