Time Limit: 2000/1000 MS
(Java/Others) Memory Limit: 65536/32768 K
(Java/Others)
Total Submission(s): 4543 Accepted
Submission(s): 1108
,
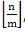which means he ignores the rest interviewees (poor guys because they comes
late). Then, each segment is assigned to an interviewer and the interviewer
chooses the best one from them as the employee.
题意：
给出n个数，分成m段，每段取一个最大的，问m最小为多少时每段取到的最大的数的和大于K。
RMQ+二分：
时间卡很紧，800+ms C++飘过。
这题有个trap，坑了我很久的trap。
RMQ+二分其实很快就写好了，问题是卡在数据上，先看看数据
11 300
7 100 7 101 100 100 9 100 100 110 110
10 1500
1 1 1 1 1000 1000 1 1 1 1
8 201
100 100 100 100 101 100 100 100
很明显第一组数据输出的是3，题目有解释。
到第二组数据呢？本来应该输出2才合理，可是运行结果却是输出了6.
第三组也是输出2才合理，可结果是输出了3。
个人觉得是数据有点问题，题目也有点问题，其实这题用二分过不了才对，因为看第二组和第三组数据可知，数据其实没有单调性。
贴一下代码：
1 //781MS 16708K 1338 B C++ 2 #include<stdio.h> 3 #include<math.h> 4 #define N 200005 5 int v[N]; 6 int dp[N][20]; 7 inline int Max(int a,int b) 8 { 9 return a>b?a:b; 10 } 11 void init(int n) 12 { 13 for(int i=1;i<=n;i++) 14 dp[i][0]=v[i]; 15 for(int j=1;j<20;j++) 16 for(int i=1;i+(1<<j)-1<=n;i++) 17 dp[i][j]=Max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]); 18 } 19 inline int RMQ(int l,int r) 20 { 21 int m=(int)(log(1.0*(r-l+1))/log(2.0)); 22 return Max(dp[l][m],dp[r-(1<<m)+1][m]); 23 } 24 inline int getsum(int m,int mm) 25 { 26 int sum=0; 27 for(int i=1;i+mm-1<=m*mm;i+=mm) 28 sum+=RMQ(i,i+mm-1); 29 return sum; 30 } 31 int main(void) 32 { 33 int n,k; 34 while(scanf("%d%d",&n,&k)!=EOF) 35 { 36 if(n<0 || k<0) break; 37 int sum=0; 38 int maxn=0; 39 for(int i=1;i<=n;i++){ 40 scanf("%d",&v[i]); 41 sum+=v[i]; 42 maxn=Max(maxn,v[i]); 43 } 44 if(sum<=k){ 45 puts("-1");continue; 46 } 47 if(maxn>k){ 48 puts("1");continue; 49 } 50 init(n); 51 int l=1,r=n,mid; 52 while(l!=r){ 53 mid=(l+r)/2; 54 int ans=getsum(mid,n/mid); 55 printf("*%d %d\n",mid,ans); 56 if(ans<=k) l=mid+1; 57 else r=mid; 58 } 59 printf("%d\n",l); 60 } 61 return 0; 62 } 63 /* 64 65 11 300 66 7 100 7 101 100 100 9 100 100 110 110 67 68 10 1500 69 1 1 1 1 1000 1000 1 1 1 1 70 71 8 201 72 100 100 100 100 101 100 100 100 73 74 75 */
hdu 3486 Interviewe (RMQ+二分),布布扣,bubuko.com
原文：http://www.cnblogs.com/GO-NO-1/p/3675991.html