基于采样的推理算法利用的思想是 概率 = 大样本下频率。故在获得图模型以及CPD的基础上,通过设计采样算法模拟事件发生过程,即可获得一系列事件(联合概率质量函数)的频率,从而达到inference的目的。
使用采样算法对概率图模型进行随机变量推理的前提是已经获得CPD。举个简单的例子,如果x = x1,x2,x3,x4的概率分别是a1,a2,a3,a4.则把一条线段分成a1,a2,a3,a4,之后使用Uniform采样,x落在1处,则随机变量取值为a1...依次类推,如图所示。
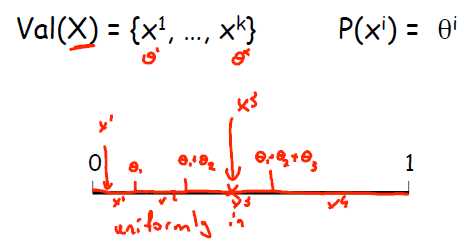
显然,采样算法中最重要的量就是采样的次数,该量会直接影响到结果的精度。关于采样次数有以下定理:

以简单的贝叶斯模型为例,如果最终关心的是联合概率,条件概率,单一变量的概率都可以使用采样算法。
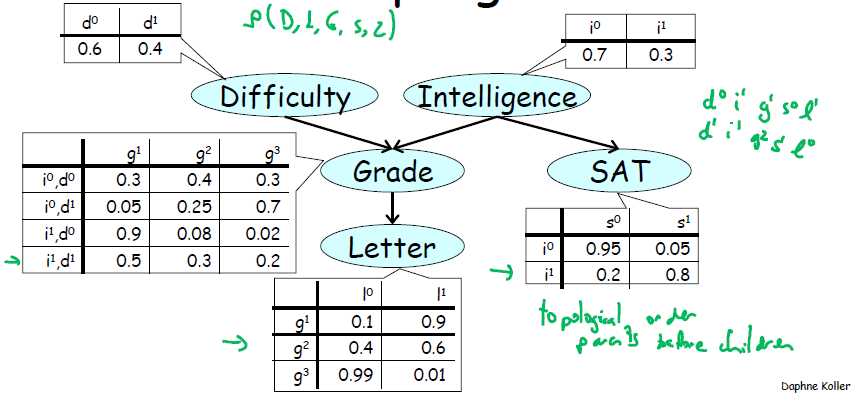
下图共需要设置 1+1+4+2+3 =11 个uniform采样器,最终得到N个结果组合(d0i1g1s0l1等)。最后计算每个组合出现的频率即可获得联合概率分布。通过边缘化则可获得单一变量概率。如果是条件概率,则去除最终结果并将符合条件的取出,重新归一化即可。
总结可知,采样算法有以下性质:
1.精度越高,结果越可靠,需要的采样次数也越多。
2.所关心的事件发生的概率很小,则需要很大的采样次数才能得到较为准确的结果。
3.如果随机变量的数量很多,则采样算法会非常复杂。故此算法不适用于随机变量很多的情况。
马尔科夫链是一种时域动态模型,其描述的随机变量随着时间的推进,在不同状态上跳跃。实际上,不同的状态是随机变量所可能的取值,相邻状态之间是相关关系。引入马尔科夫链的目的是为了描述某些情况下,随机变量的分布无法用数学公式表达,而可利用马尔科夫链进行建模。马尔科夫链如下图所示:
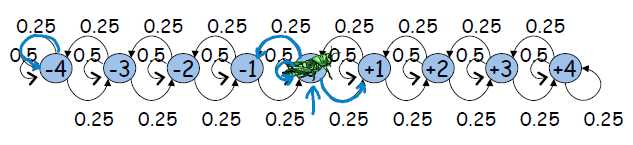
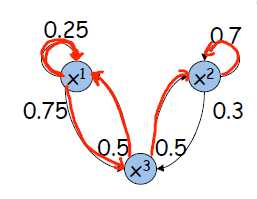
显然,对于简单的马尔科夫链我们大致还可以猜到或者通过方程解出CPD,但是一旦变量非常复杂,则我们很难获得CPD了。左图实际上是均匀分布,右图则可通过3元1次方程组对CPD进行求解。
马尔科夫链通过多次迭代后可以达到收敛的效果,如果要马尔科夫链收敛,则有以下两点要求:
1.马尔科夫链不允许有管进不管出的环
2.任何一个状态必须有回到自身的回路
使用马尔科夫链的前提是马尔科夫链已经收敛(mixed)。实际上,判断马尔科夫链迭代收敛是一件不可能的事情,而判断其未迭代收敛却是简单的。
1.对于马尔科夫链而言,蚱蜢落在相邻窗口的次数应该是相近的(因为总是在相邻窗口中跳跃)
2.蚱蜢从任意状态出发,最终收敛的结果应该是相近的。
一旦马尔科夫链迭代收敛,实际上我们得到了变量 x 的分布。
算法:
A<迭代收敛>
1. 选择不同的状态C个作为初始点(故有C条链)
2. 概率迭代T次(C条链同时进行)
3. 对比不同链条的相同窗口,观察次数是否相近
4. 假设马尔科夫链已经收敛
B<采样推理>
1.选择一个初始状态
2.依据转移概率计算所得采样
3.将所得采样放入采样结果集合中
4.利用采样结果集合计算所需要的量
原文:http://www.cnblogs.com/ironstark/p/5229085.html