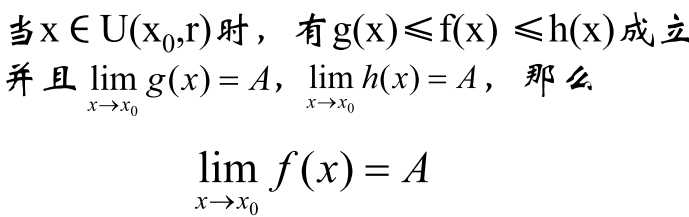
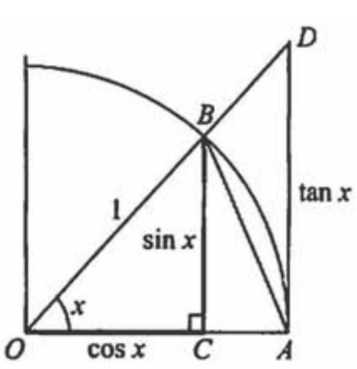
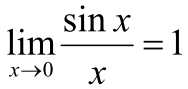
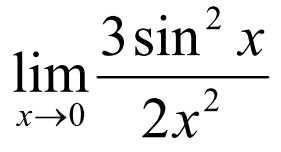 = 3/2
= 3/2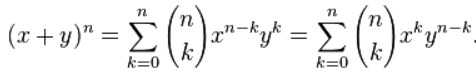

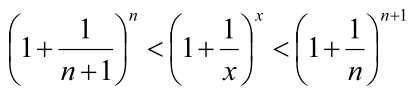
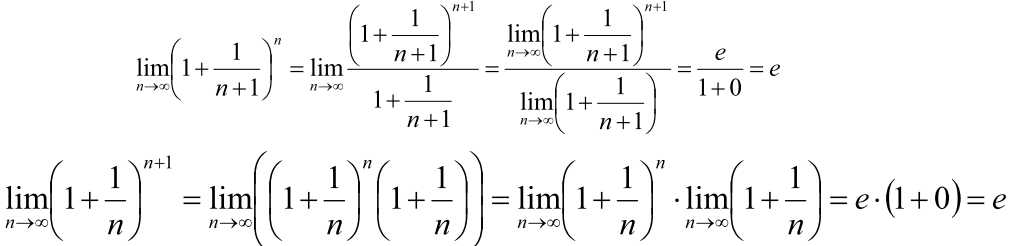
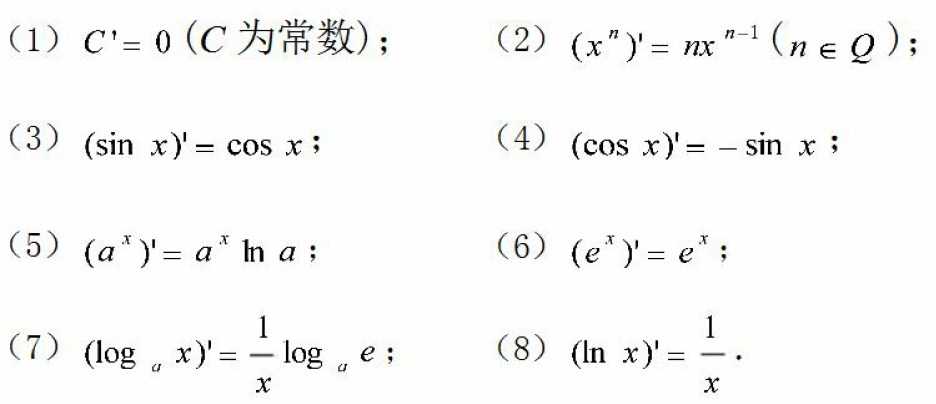

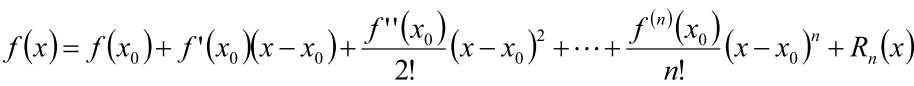
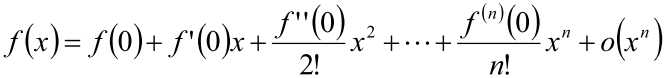
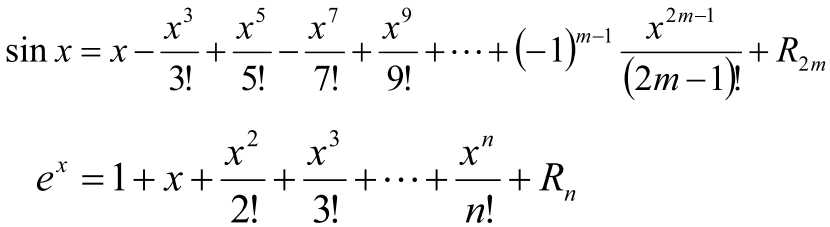
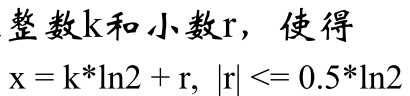
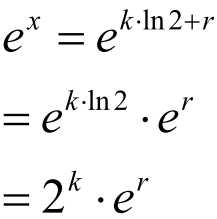
函数f(x)在任意方向L的导数,φ是L与x轴方向夹角
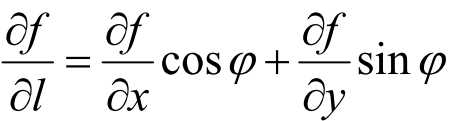
梯度,高程变化最快的方向,抛去cos,sin函数
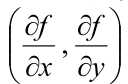
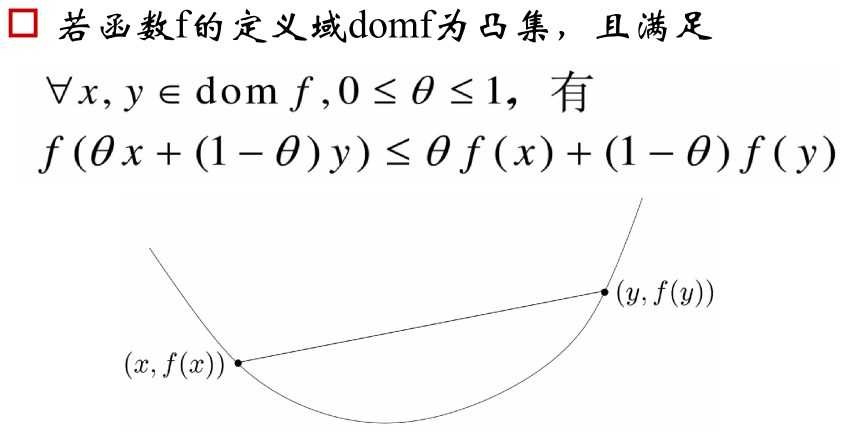
形象化解释
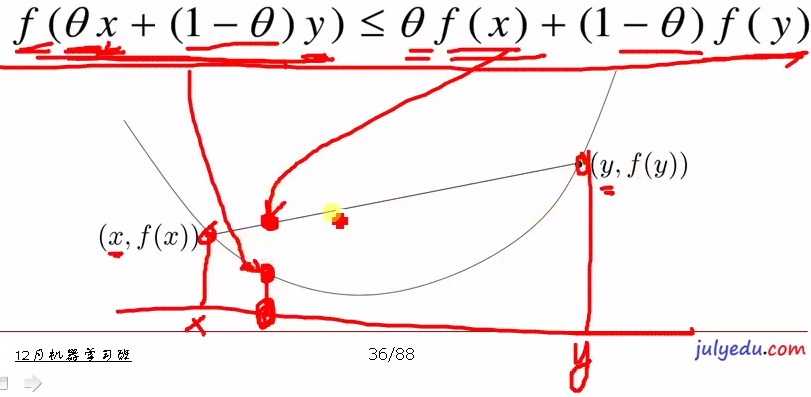
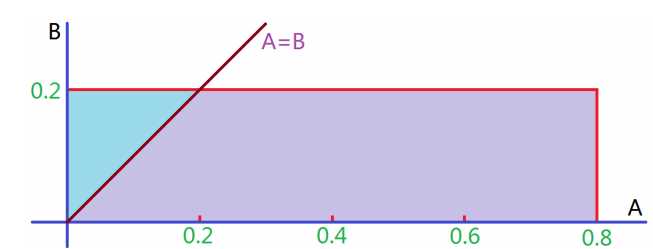
判定方法


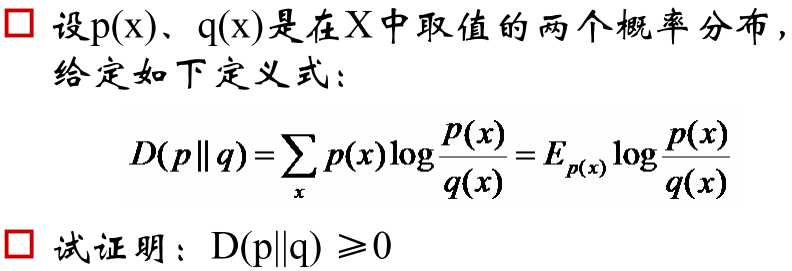

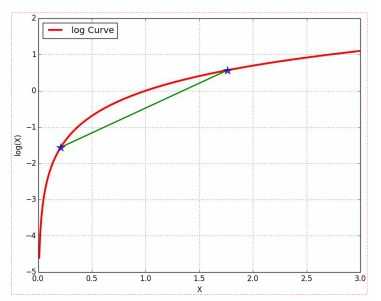

- 事件一定发生 => P(X) = 1,反之不一定成立
- 事件一定不发生 => P(X) = 0,反之不一定成立
- 即概率 = 0,不意味着不可能发生
- 离散 => 概率
- 连续变量 => 概率密度
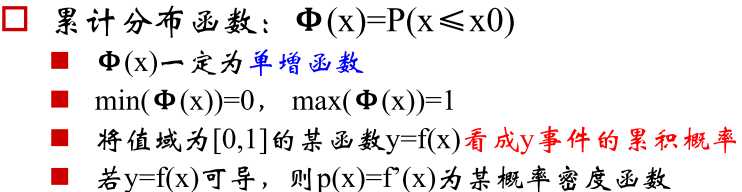
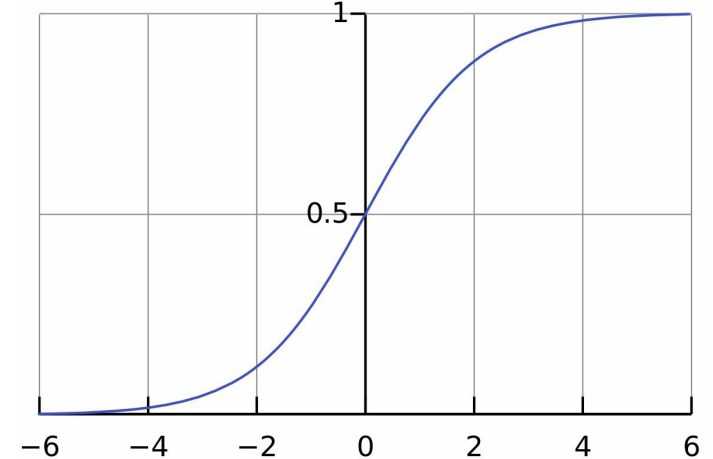
- 给出f(x),值域是[0,1] => 累计概率 => 求导,得到概率密度(Logistic回归)



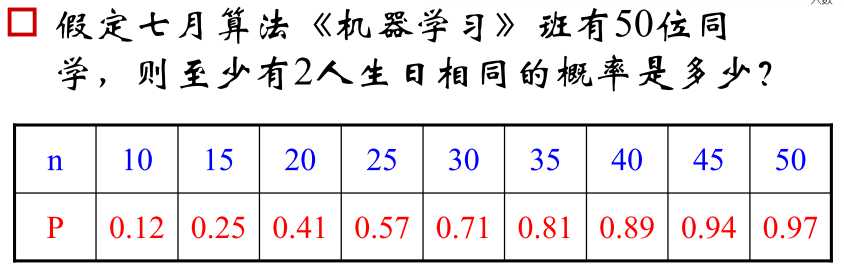

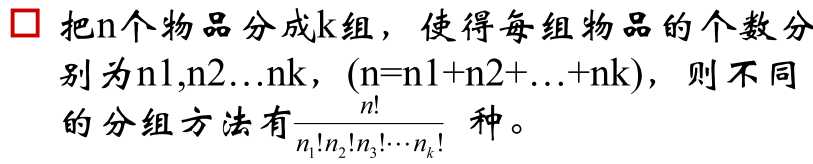
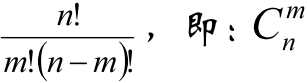




Possion分布
将e^x的展开式处理
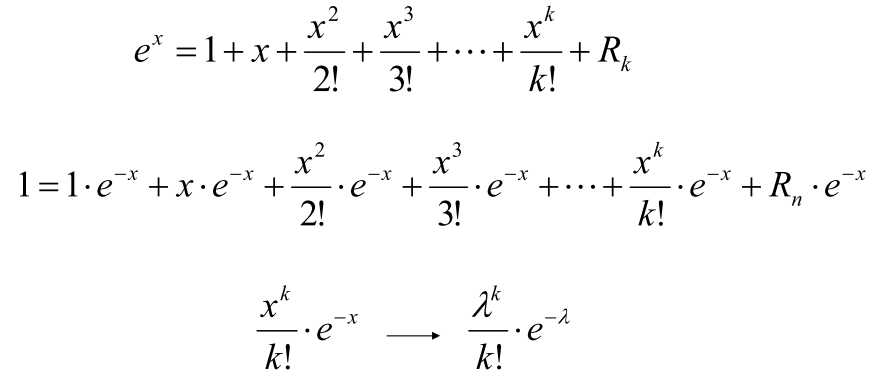
指数分布
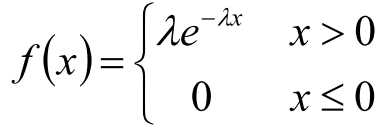
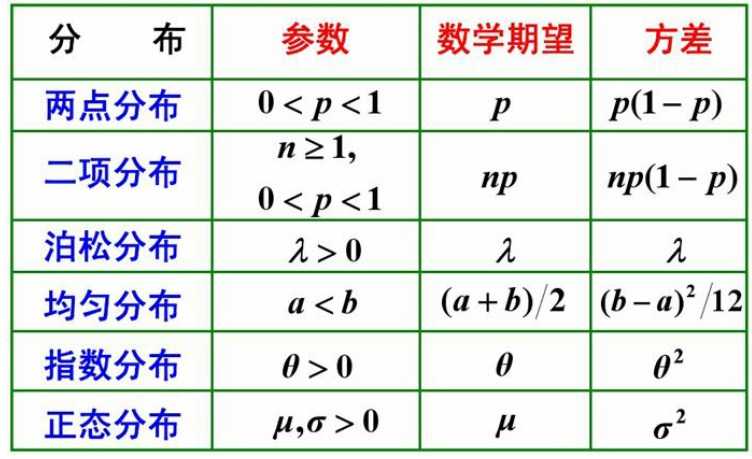
总结
用指数族 - exponential family来表达
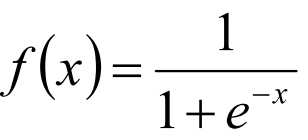
求导数
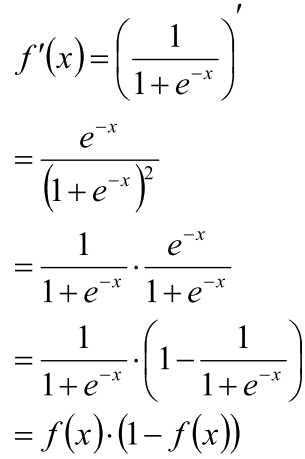
Gamma函数

原文:http://www.cnblogs.com/kongww/p/5237247.html