在这里记录一下做题中遇到的各种性质、定理,数论知识偏多,没有什么顺序,只是做到了就记录一下,不断更新。。
费马小定理是数论中的一个重要定理,其内容为: 假如p是质数,且(a,p)=1,那么 a^(p-1) ≡1(mod p)。即:假如p是质数,且a,p互质,那么a的(p-1)次方除以p的余数恒等于1。
欧拉定理,(也称费马-欧拉定理)是一个关于同余的性质。欧拉定理表明,若n,a为正整数,且n,a互质,则:
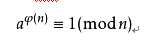
欧拉函数
定义:用于计算 p(n),比n小的所有与n互质的数。
计算公式:p(n)=n*(1-1/p1)*(1-1/p2)....*(1-1/pk)【p1,p2,pk都是n的素因子】
另:若n=p1^q1*p2^q2*.....*pk^qk
则,p(n)=(p1-1)*p1^(q1-1)*(p1-1)*p2^(q2-1)......*(pk-1)*pk^(qk-1)
性质:若m,n互质,φ(mn)=φ(m)φ(n)。当n为奇数时,φ(2n)=φ(n)
欧拉定理:
a,m互质,a^φ(m)≡1(mod m)
例:2,3互质,那么,2^2%3=1
推论:对于互质的数a、n,满足a^(φ(n)+1) ≡ a (mod n)
欧拉公式的延伸:小于n 与n互质的数的和 是euler(n)*n/2
多个数的最小公倍数 每个数分解因子 质因子最高次幂相乘之积
对于任何正整数x,其约数的个数记做g(x).例如g(1)=1,g(6)=4.如果某个正整数x满足:对于任意i(0<i<x),都有g(i)<g(x),则称x为反素数.
性质一:一个反素数的质因子必然是从2开始连续的质数.
性质二:p=2^t1*3^t2*5^t3*7^t4.....必然t1>=t2>=t3>=....
约瑟夫: f[1] = 0; f[i] = (f[i-1]+m)%i;
高次幂取模: a^b%c = a ^(b%eular(c)+eular(c)) % c。 eular(c)为欧拉函数
原文:http://www.cnblogs.com/shangyu/p/3677457.html