参照:http://www.cnblogs.com/liangyan19910818/archive/2011/08/26/2153926.html#3259652
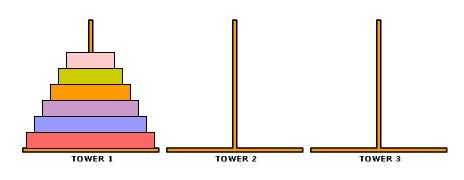
f(n):原始A柱有n个圆盘,全部移动到C柱的移动次数
A柱上的n-1个圆盘从A->B需要f(n-1)次移动,第n个圆盘移动到C柱一次,
再把B柱上的n-1个圆盘从B->C仍然需要f(n-1)次移动
容易得到f(n) =2*f(n-1)+1(n>=2),f(1) = 1从而递推可得
f(n) = 2^n -1
/* 思路: 当n=1,圆盘1将顺着大部分圆盘的方向移动 否则,先将A上的前n-1个圆盘从A借助C移动到B,然后将第n个圆盘直接移动到柱C 对B柱上的n-1个圆盘进行相似的操作移动到C,这是很明显的递归 */ #include <stdio.h> void move(char x,char y,int i) { static int j = 0; printf("%d: %d from %c to %c\n",++j,i,x,y); } void Hanoi(char x,char y,char z,int n) { if(n == 1) { move(x,z,n); return; } else{ Hanoi(x,z,y,n-1); move(x,z,n); Hanoi(y,x,z,n-1); } } int main() { int n; scanf("%d",&n); Hanoi(‘A‘,‘B‘,‘C‘,n); return 0; }
原文:http://www.cnblogs.com/520xiuge/p/5243842.html