题意:按顺时针顺序给你n个顶点的坐标,这些顶点构成了一堵闭合的墙,现在要求在这堵墙之外再起一堵墙
且两堵墙之间至少相距l的距离,求新起得墙的最小长度;
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <vector>
#include <queue>
#include <map>
#include <algorithm>
#include <set>
using namespace std;
#define MM(a) memset(a,0,sizeof(a))
typedef long long ll;
typedef unsigned long long ULL;
const int mod = 1000000007;
const double eps = 1e-10;
const int inf = 0x3f3f3f3f;
const int big=50000;
const double pi=acos(-1);
int max(int a,int b) {return a>b?a:b;};
int min(int a,int b) {return a<b?a:b;};
struct node{
int x, y;
}ne[50005];
bool cmp(node a,node b)
{
if(a.x!=b.x)
return a.x<b.x;
return a.y<b.y;
}
int cross(node a,node b,node c)
{
return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}
int a[50005],m,k;
void tubao(int n)
{
sort(ne+1,ne+n+1,cmp);
m=0;
for(int i=1;i<=n;i++)
{
while(m>=2&&cross(ne[a[m-1]],ne[a[m]],ne[i])<=0)
m--;
++m;
a[m]=i;
}
k=m;
for(int i=n-1;i>=1;i--)
{
while((m>=k+1)&&cross(ne[a[m-1]],ne[a[m]],ne[i])<=0)
m--;
++m;
a[m]=i;
}
}
double dist(int i,int j)
{
return sqrt((ne[i].x-ne[j].x)*(ne[i].x-ne[j].x)
+(ne[i].y-ne[j].y)*(ne[i].y-ne[j].y));
}
int main()
{
int n,l;
while(~scanf("%d %d",&n,&l))
{
for(int i=1;i<=n;i++)
scanf("%d %d",&ne[i].x,&ne[i].y);
tubao(n);
//for(int i=1;i<=m;i++)
// cout<<"|||"<<i<<": "<<a[i]<<endl;
double ans=0;
for(int i=1;i<=m-1;i++)
ans+=dist(a[i],a[i+1]);
ans+=dist(a[m],a[1]);
ans+=2*pi*l+0.5;
printf("%d\n",int(ans));
}
return 0;
}
分析:思维题,看到离墙最少距离,就想着每面墙外移l距离,然后求边长,其实这样算出来不是最短的
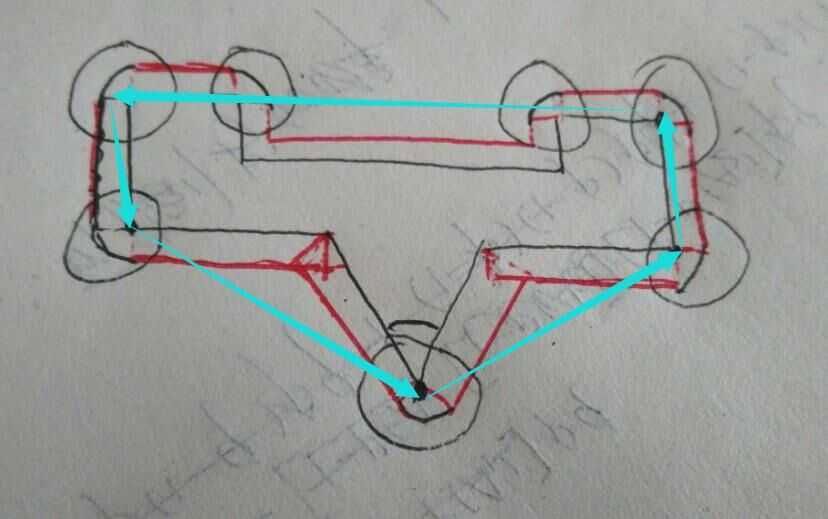
看图,求凸包加个圆就好;
是把蓝色的部分外移l,而不是算红色的部分
原文:http://www.cnblogs.com/smilesundream/p/5244390.html