在m*n的一个长方形方格中,用一个1*2的骨牌排满方格。问有多少种不同的排列方法。(n <= 5) ? 例如:3 * 2的方格,共有3种不同的排法。(由于方案的数量巨大,只输出 Mod 10^9 + 7 的结果)
Input 2个数M?N,中间用空格分隔(2?<=?m?<=?10^9,2?<=?n?<=?5) Output 输出数量?Mod?10^9?+?7 Input示例 2?3 Output示例 3 |
?
把别人的代码研究了一下,发现他的思想是这样的:
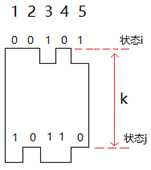
对于n为5的情况:结合代码看下图, dp[i][j]表示的意义是在连续的k长的一段中,首部状态是i,尾部状态是j的组成的图形中,一共有多少种铺砖方法,这里的k实际上就是dp=dp*dp运算了k次,可以结合矩阵和图的联系去理解。
在函数dfs中完成对dp的初始化,此时k实际上是1,然后计算出dp^(m+1)的值就行了。
?
?
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> using namespace std; typedef long long ll; const int mod=1e9+7; ll dp[1<<5][1<<5]; int m,n; ? void dfs(int col,int pre,int now) { if(col>n) return; if(col==n) { dp[pre][now]++; return; } //在这里没有做好!为什么这里只用三个dfs,是因为如果加上后两个就会有重复了。 //认真考虑一下还是可以相对的 dfs(col+1,pre<<1,(now<<1)|1); dfs(col+1,(pre<<1)|1,now<<1); dfs(col+2, pre<<2 , now<<2); //dfs(col+2, pre<<2 , (now<<2)|3); //dfs(col+2, (pre<<2)|3 , now<<2); } void mul(ll ret[1<<5][1<<5],ll a[1<<5][1<<5],ll b[1<<5][1<<5]){ for(int i=0;i<(1<<n);i++) for(int j=0;j<(1<<n);j++){ ll tmp=0; for(int k=0;k<(1<<n);k++) { tmp+=a[i][k]*b[k][j]; tmp%=mod; } ret[i][j]=tmp; } } int main() { scanf("%d%d",&m,&n); memset(dp,0,sizeof(dp)); dfs(0,0,0); for(int i=0;i<(1<<n);i++) { for(int j=0;j<(1<<n);j++) { //printf("%d ",dp[i][j]); } puts(""); } ? ll ret[1<<5][1<<5]; ll tmp[1<<5][1<<5]; memset(ret,0,sizeof(ret)); for(int i=0;i<(1<<n);i++) ret[i][i]=1; m++; while(m) { for(int i=0;i<(1<<n);i++) for(int j=0;j<(1<<n);j++) tmp[i][j]=ret[i][j]; if(m&1) { mul(ret,tmp,dp); } m=m>>1; mul(tmp,dp,dp); for(int i=0;i<(1<<n);i++) for(int j=0;j<(1<<n);j++) dp[i][j]=tmp[i][j]; } cout<<ret[0][(1<<n)-1]<<endl; } |
原文:http://www.cnblogs.com/lastone/p/5261548.html