双边滤波(Bilateral filter)是一种非线性的滤波方法,是结合图像的空间邻近度和像素值相似度的一种折衷处理,同时考虑空域信息和灰度相似性,达到保边去噪的目的。具有简单、非迭代、局部的特点。
双边滤波器的好处是可以做边缘保存(edge preserving),一般过去用的维纳滤波或者高斯滤波去降噪,都会较明显地模糊边缘,对于高频细节的保护效果并不明显。双边滤波器顾名思义比高斯滤波多了一个高斯方差sigma-d,它是基于空间分布的高斯滤波函数,所以在边缘附近,离的较远的像素不会太多影响到边缘上的像素值,这样就保证了边缘附近像素值的保存。但是由于保存了过多的高频信息,对于彩色图像里的高频噪声,双边滤波器不能够干净的滤掉,只能够对于低频信息进行较好的滤波。
滤波算法中,目标点上的像素值通常是由其所在位置上的周围的一个小局部邻居像素的值所决定。在2D高斯滤波中的具体实现就是对周围的一定范围内的像素值分别赋以不同的高斯权重值,并在加权平均后得到当前点的最终结果。而这里的高斯权重因子是利用两个像素之间的空间距离(在图像中为2D)关系来生成。通过高斯分布的曲线可以发现,离目标像素越近的点对最终结果的贡献越大,反之则越小。其公式化的描述一般如下所述:
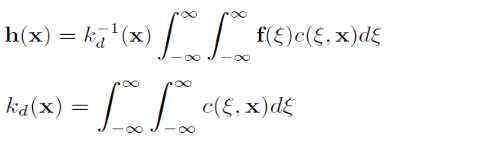
其中的c即为基于空间距离的高斯权重,而用来对结果进行单位化。
高斯滤波在低通滤波算法中有不错的表现,但是其却有另外一个问题,那就是只考虑了像素间的空间位置上的关系,因此滤波的结果会丢失边缘的信息。这里的边缘主要是指图像中主要的不同颜色区域(比如蓝色的天空,黑色的头发等),而Bilateral就是在Gaussian blur中加入了另外的一个权重分部来解决这一问题。Bilateral滤波中对于边缘的保持通过下述表达式来实现:
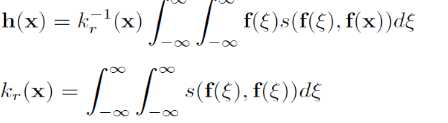
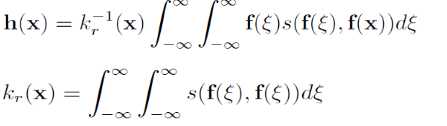
其中的s为基于像素间相似程度的高斯权重,同样用来对结果进行单位化。对两者进行结合即可以得到基于空间距离、相似程度综合考量的Bilateral滤波:
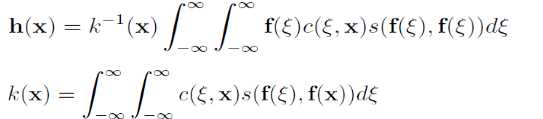
上式中的单位化分部综合了两种高斯权重于一起而得到,其中的c与s计算可以详细描述如下:
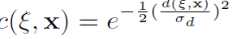
且有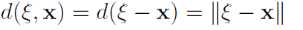
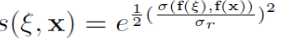
且有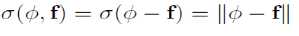
上述给出的表达式均是在空间上的无限积分,而在像素化的图像中当然无法这么做,而且也没必要如此做,因而在使用前需要对其进行离散化。而且也不需要对于每个局部像素从整张图像上进行加权操作,距离超过一定程度的像素实际上对当前的目标像素影响很小,可以忽略的。限定局部子区域后的离散化公就可以简化为如下形式:
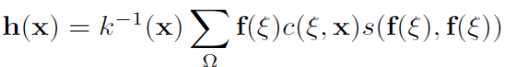
上述理论公式就构成了Bilateral滤波实现的基础。为了直观地了解高斯滤波与双边滤波的区别,我们可以从下列图示中看出依据。假设目标源图像为下述左右区域分明的带有噪声的图像(由程序自动生成),蓝色框的中心即为目标像素所在的位置,那么当前像素处所对应的高斯权重与双边权重因子3D可视化后的形状如后边两图所示:
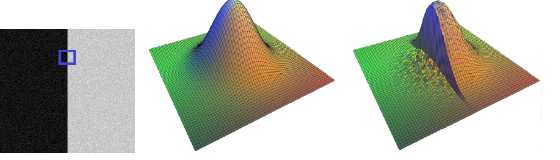
左图为原始的噪声图像;中间为高斯采样的权重;右图为Bilateral采样的权重。从图中可以看出Bilateral加入了相似程度分部以后可以将源图像左侧那些跟当前像素差值过大的点给滤去,这样就很好地保持了边缘。为了更加形象地观察两者间的区别,使用Matlab将该图在两种不同方式下的高度图3D绘制出来,如下:
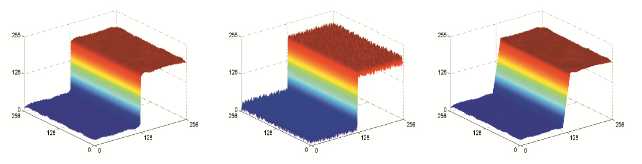
上述三图从左到右依次为:双边滤波,原始图像,高斯滤波。从高度图中可以明显看出Bilateral和Gaussian两种方法的区别,前者较好地保持了边缘处的梯度,而在高斯滤波中,由于其在边缘处的变化是线性的,因而就使用连累的梯度呈现出渐变的状态,而这表现在图像中的话就是边界的丢失(图像的示例可见于后述)。
有了上述理论以后实现Bilateral Filter就比较简单了,其实它也与普通的Gaussian Blur没有太大的区别。这里主要包括3部分的操作: 基于空间距离的权重因子生成;基于相似度的权重因子的生成;最终filter颜色的计算。
这就是通常的Gaussian Blur中使用的计算高斯权重的方法,其主要通过两个pixel之间的距离并使用如下公式计算而来:
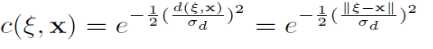
与基于距离的高斯权重计算类似,只不过此处不再根据两个pixel之间的空间距离,而是根据其相似程度(或者两个pixel的值之间的距离)。
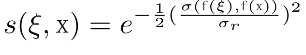
其中的表示两个像素值之间的距离,可以直接使用其灰度值之间的差值或者RGB向量之间的欧氏距离。
其中的相似度分部的权重s主要根据两个Pixel之间的颜色差值计算面来。对于灰度图而言,这个差值的范围是可以预知的,即[-255, 255],因而为了提高计算的效率我们可以将该部分权重因子预计算生成并存表,在使用时快速查询即可。使用上述实现的算法对几张带有噪声的图像进行滤波后的结果如下所示:
原文:http://www.cnblogs.com/qiqibaby/p/5296681.html