|
术语
|
解释
|
|
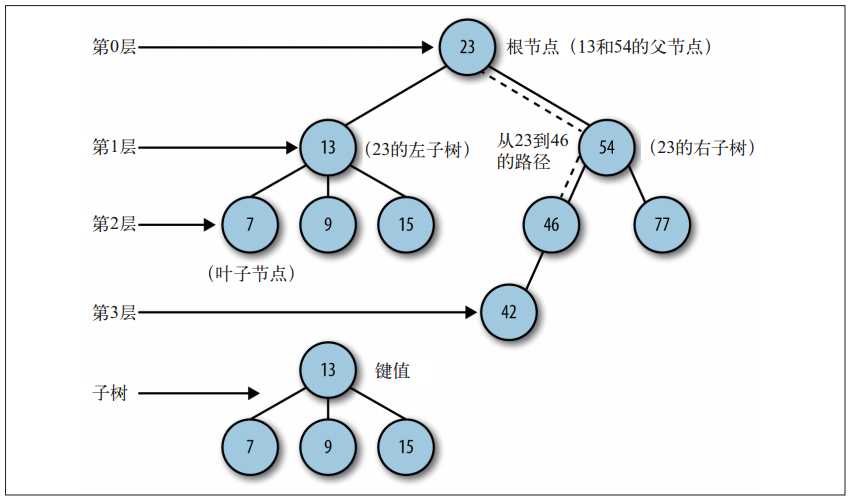
节点
|
树中的每个元素
|
|
根节点
|
树顶部的节点,没有父节点
|
|
内部节点
|
至少有一个子节点的节点
|
|
外部节点(叶节点)
|
没有子元素的节点
|
|
子树
|
由节点和它的后代构成
|
|
深度
|
节点的一个属性,取决于它的祖先节点的数量
|
|
高度
|
取决于所有节点深度的最大值
|

|
序号
|
方法
|
说明
|
|
1
|
insert(key) | 向树中插入一个新的键 |
|
2
|
search(key) | 在树中查找一个键,如果节点存在,则返回 true;如果不存在,则返回 false |
|
3
|
inOrderTraverse | 通过中序遍历方式遍历所有节点 |
|
4
|
preOrderTraverse | 通过先序遍历方式遍历所有节点 |
|
5
|
postOrderTraverse | 通过后序遍历方式遍历所有节点 |
|
6
|
min |
返回树种最小的值/键
|
|
7
|
max | 返回树种最大的值/键 |
|
8
|
remove(key) | 从树中移除某个键 |

1 function BinarySearchTree() { 2 // 辅助类Node定义 3 var Node = function(key) { 4 this.key = key; 5 this.left = null; 6 this.right = null; 7 } 8 var root = null; 9 10 // 向树中插入一个新的键 11 this.insert = function(key) { 12 var newNode = new Node(key); 13 14 if (root === null) { 15 root = newNode; 16 } else { 17 insertNode(root, newNode); // 私有的辅助函数 18 } 19 } 20 21 this.insertNode = function(node, newNode) { 22 if (newNode.key < node.key) { 23 if (node.left === null) { 24 node.left = newNode; 25 } else { 26 insertNode(node.left, newNode); // 如果有左侧子节点,则通过递归调用继续找到树的下一层 27 } 28 } else { 29 if (node.right === null) { 30 node.right = newNode; 31 } else { 32 insertNode(node.right, newNode); // 如果有右侧子节点,则通过递归调用继续找到树的下一层 33 } 34 } 35 } 36 37 /* 中序遍历 38 * inOrderTraverse方法接收一个回调函数作为参数。 39 * 回调函数用来定义我们对遍历到的每个节点进行的操作(也叫访问者模式) 40 */ 41 this.inOrderTraverse = function(callback) { 42 inOrderTraverseNode(root, callback); 43 } 44 45 this.inOrderTraverseNode = function(node, callback) { 46 if (node !== null) { 47 inOrderTraverseNode(node.left, callback); 48 callback(node.key); 49 inOrderTraverseNode(node.right, callback); 50 } 51 } 52 53 // 先序遍历 54 this.preOrderTraverse = function(callback) { 55 preOrderTraverseNode(root, callback); 56 } 57 58 this.preOrderTraverseNode = function(node, callback) { 59 if (node !== null) { 60 callback(node.key); 61 preOrderTraverseNode(node.left, callback); 62 preOrderTraverseNode(node.right, callback); 63 } 64 } 65 66 // 后序遍历 67 this.postOrderTraverse = function(allback) { 68 postOrderTraverseNode(root, callback); 69 } 70 71 this.postOrderTraverseNode = function(node, callback) { 72 if (node !== null) { 73 postOrderTraverseNode(node.left, callback); 74 postOrderTraverseNode(node.right, callback); 75 callback(node.key); 76 } 77 } 78 79 // 搜索树中的最小值 80 this.min = function() { 81 return minNode(root); 82 } 83 84 var minNode = function(node) { 85 if (node) { 86 while (node && node.left !== null) { 87 node = node.lfet; 88 } 89 return node.key; 90 } 91 return null; 92 } 93 94 // 搜索树中的最大值 95 this.max = function() { 96 return maxNode(root); 97 } 98 99 this.maxNode = function(node) { 100 if (node) { 101 while (node && node.right !== null) { 102 node = node.right; 103 } 104 return node.key; 105 } 106 return null; 107 } 108 109 // 搜索树中的特定值 110 this.search = function(key) { 111 return searchNode(root, key); 112 } 113 114 var searchNode = function(node, key) { 115 if (node === null) { 116 return false; 117 } 118 if (key < node.key) { 119 return searchNode(node.left ,key); 120 } else if (key > node.key) { 121 return searchNode(node.right, key); 122 } else { 123 return true; 124 } 125 } 126 127 // 从树中移除某个键 128 this.remove = function(key) { 129 root = removeNode(root, key); // root被赋值为removeNode方法的返回值 130 } 131 132 var removeNode = function(node, key) { 133 if (node === null) { // 键不存在于树中,则返回null 134 return null; 135 } 136 if (key < node.key) { // 如果要找的键比当前节点的值小,就沿着树的左边找到下一个节点 137 node.left = removeNode(node.left, key); 138 return node; 139 } else if (key > node.key) { // 如果要找的键比当前节点的值大,就沿着树的左边找到下一个节点 140 node.right = removeNode(node.right, key); 141 return node; 142 } else { // 键等于node.key 143 144 // 第一种情况——一个叶节点 145 if (node.left === null && node.right === null) { 146 node = null; 147 return node; 148 } 149 150 // 第二种情况——一个只有一个子节点的节点 151 if (node.left === null) { 152 node = node.right; 153 return node; 154 } else if (node.right === null) { 155 node = node.left; 156 return node; 157 } 158 159 // 第三种情况——一个有两个子节点的节点 160 var aux = findMinNode(node.right); 161 node.key = aux.key; // 用右侧子树中的最小节点的键去更新这个节点的值 162 node.right = removeNode(node.right, aux.key); // 移除右侧子树中的最小节点 163 return node; 164 } 165 } 166 }
原文:http://www.cnblogs.com/Ruth92/p/5328333.html