快速排序

快速排序的原理很简单

1.从数组中选出一个数F，然后对于这个数组中的其他数，根据大小，将其分成左(L)右(R)两部分，形成一个新的数组(LFR)。

2.对于L和R继续进行快速排序。（递归）

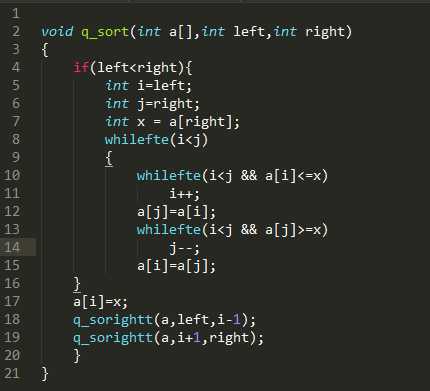
其实快排的思想很简单，但是并不是特别的容易理解具体的实现的。

这也是快排的重点，它先将一个数存到基准x（最右边）中，（假设是从大到小的排序），然后从左边依次开始找到一个小于x的数a[i]，存到最右边中，于是a[i]和a[right]此时相等，再从右边依次开始找到一个大于x的数，将其存到a[i]中，依次类推，直到i和j重合。

这就是最基本的快速排序。

快速排序的优化：

1.如果出现了一种很极端的情况，比如每次左右两边数组都分布不均衡，就比如一个已排好的序列，那么假设每次都是将最右边的数（或者最左边的额数）作为基准，那么应该需要n-1次比较才能排完，这个时候的时间复杂度会达到O(n^2)，而假设每次取得数都是最中间的数，那么只需要logn次就能拍完，时间复杂度是O(nlogn),但是在绝大多数情况下，时间复杂度是趋于O(nlogn),因此只需要尽量的让基准随机，那么我们就可以得到接近于O(nlogn)的时间复杂度。

　　基于这种情况，我们可以让随机化基准，让出现最差的情况的概率降低。

2.在序列长度很小的时候，会发现快排的效率会降低，于是我们可以采用堆排序或者插入排序（在基数比较少的情况下，时间复杂度接近于O(n)）

3.还有其他的优化如：三平均法等等。

快速排序

原文：http://www.cnblogs.com/muzhiwan/p/5330447.html