分治法(divide and conquer)
Merge sort;
cal X^n;
Fabonacci : F(n) = F(n - 1) + F(n - 2)(F(0) = 0, F(1) = 1;)
1,如果直接递归,可以看出,递归树不对称,且下降的速度是线性的,Time将 是指数级别的T(n) = (a)^n, a是黄金分割数。
2,自底向上的,先算F(1),F(2),F(3),...,F(N),T(n) = n;是线性的。
3,利用矩阵乘法的平方,时间和计算x^n一样是Lg(n)
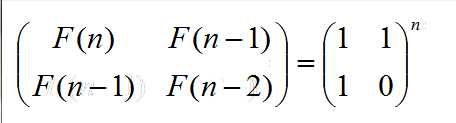
(归纳法可证)
Matrix multiplication.
Input: A[aij], B[bij];
Output:C[cij];
常规思路,T(n^3)
分治法:1,矩阵分块。T(n) = 8T(n/2) + θ(n^2) = T(n^3)(主方法c1)
no better
2,strassen‘s algotithm:减少子矩阵乘法的次数。(8->7)T(n) = T(n^lg7) = T(n^2.81)
原文:http://www.cnblogs.com/stormhan/p/5332627.html