1.赋范线性空间和内积空间
在线性代数的初级教材里,一般是在向量空间中定义内积,然后再由内积来导出范数,比如在n维实向量空间中:
|x||=√<x,x>
在线性代数的高级教材中,一般是将内积和范数单独来定义的,而这之间可能并没有直接的关系。在向量空间中引入范数,可以得到一个赋范线性空间(normed linear space),在向量空间中引入内积,可以得到一个内积空间(inner product space).定义如下:
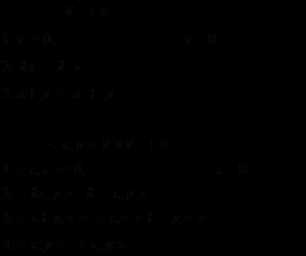
cauchy-schwarz不等式

给定一个内积空间,可以定义一个范数:||x||=<x,x>½ 一般把这个范数叫做由内积导出的范数。可以发现,如果给内积空间加入一个由内积导出的范数,那么这个内积空间就是一个赋范线性空间。这个赋范线性空间有以下特殊的性质,这些性质是普通的赋范线性空间所不具有的:

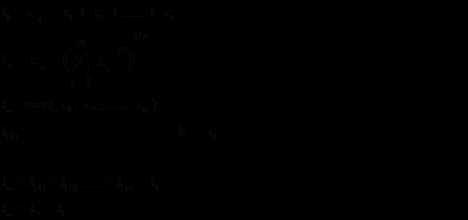
上面已经看到了,在向量空间V中,存在多个实值函数满足范数公理,也就是说存在多个范数,一个很自然的问题就是,这些范数之间具有什么样的关系,有如下两个重要定理:范数等价性和完备性。
有限维赋范线性空间中的范数是等价的:

有限维赋范线性空间是完备的:

原文:http://www.cnblogs.com/francisYoung/p/5358894.html