作者：樱花猪
摘要：
本文为七月算法（julyedu.com）12月机器学习第八次次课在线笔记。聚类算法是一种常见的无监督的学习方法，概念简单在图像、机器学习中都有应用。目前有许多聚类方法，本次课程将一一探讨各种各样的聚类算法。
引言：
聚类算法在很早就接触过，简单的说就是通过对于某些相关性的测量来将样本分成不同的类别，聚类算法除了在机器学习中有所应用在图像分割时也是一种非常好的思路。本次课程从我们熟悉的K-means聚类开始讲起，介绍了层次聚类、密度聚类、谱聚类等方法。文章的最后还介绍了随机游走与标签传递算法。这次课程内容简单却又非常的实用。
预备知识：
矩阵论；熵；
聚类
K-means
二分K均值聚类；轮廓系数；
层次聚类
凝聚的层次聚类（AGENS）算法；分裂的层次聚类（DIANA）算法
密度聚类
DBSCAN算法；密度最大值聚类；
谱聚类
未正则拉普拉斯矩阵；随机游走拉普拉斯矩阵;对称拉普拉斯矩阵；
标签传递算法
一、聚类
1、聚类定义
聚类就是对大量未知标注的数据集，按数据的内在相似性将数据集划分为多个类别，使类别内的数据相似度较大而类别间的数据相似度较小。聚类是一种无监督的学习方法。（无监督：没有标准答案）
2、相似度/距离计算方法总结
需要关注这些相似度之间的关系、公式意义和优化计算方法。
3、聚类的基本思想
对于给定的类别数目k，首先给出初始划分，通过迭代改变样本和簇的隶属关系，使得每一次改进之后的划分方案都较前一次好。
二、K-mean算法
K-means算法，也被称为k-平均或k-均值，是一种广泛使用的聚类算法，或者成为其他聚类算法的基础。
1、算法步骤：
a. 初始化聚类中心个数和聚类中心点。
b. 对于每个样本将其标记为距离类别中心最近的类。
c. 将每个类别中心更新为隶属该类别的所有样本的均值。
d. 重复最后两步，直到类别中心的变化小于某阈值。
中止条件：迭代次数/簇中心变化率/最小平方误差MSE(MinimumSquaredError)
2、改进方案：二分K均值聚类
将内间距大的类分开，将内间距小两个类之间聚类大的合并。
3、K-means聚类方法总结
优点：
a. 是解决聚类问题的一种经典算法，简单、快速
b. 对处理大数据集，该算法保持可伸缩性和高效率
c. 当簇近似为高斯分布时，它的效果较好
缺点：
a. 在簇的平均值可被定义的情况下才能使用，可能不适用于某些应用
b. 必须事先给出k(要生成的簇的数目)，而且对初值敏感，对于不同的初始值，可能会导致不同结果。
c. 不适合于发现非凸形状的簇或者大小差别很大的簇
d. 对躁声和孤立点数据敏感
可作为其他聚类方法的基础算法，如谱聚类
4、轮廓系数(Silhouette)
根据样本i的簇内不相似度ai和簇间不相似度bi，定义样本i的轮廓系数：
接近1，则说明样本i聚类合理；
接近-1，则说明样本i更应该分类到另外的簇；若
近似为0，则说明样本i在两个簇的边界上
所有样本的
的均值称为聚类结果的轮廓系数，是该聚类是否合理、有效的度量。
三、层次聚类方法
1、概述：
层次聚类方法对给定的数据集进行层次的分解，直到某种条件满足为止。具体又可分为
凝聚的层次聚类：AGNES算法：一种自底向上的策略，首先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，直到某个终结条件被满足。
分裂的层次聚类：DIANA算法：采用自顶向下的策略，它首先将所有对象置于一个簇中，然后逐渐细分为越来越小的簇，直到达到了某个终结条件。
2、凝聚的层次聚类（AGENS）算法
AGNES(AGglomerativeNESting)算法最初将每个对象作为一个簇，然后这些簇根据某些准则被一步步地合并。两个簇间的距离由这两个不同簇中距离最近的数据点对的相似度来确定；聚类的合并过程反复进行直到所有的对象最终满足簇数目。
DIANA(DIvisiveANAlysis)算法是上述过程的反过程，属于分裂的层次聚类，首先将所有的对象初始化到一个簇中，然后根据一些原则(比如最大的欧式距离)，将该簇分类。直到到达用户指定的簇数目或者两个簇之间的距离超过了某个阈值。
四、密度聚类方法
1、概述：
密度聚类方法的指导思想是，只要样本点的密度大于某阈值，则将该样本添加到最近的簇中。
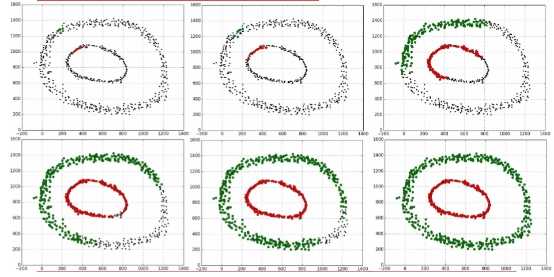
（优点）这类算法能克服基于距离的算法只能发现“类圆 形”(凸)的聚类的缺点，可发现任意形状的聚类，且对噪声数据不敏感。（缺点）但计算密度单元的计算复杂度大，需要建立空间索引来降低计算量。
2、DBSCAN算法
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
一个比较有代表性的基于密度的聚类算法。 与划分和层次聚类方法不同，它将簇定义为 密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在有“噪声”的数据中发现任意形状的聚类
算法流程：
a. 如果一个点p的ε-邻域包含多于m个对象，则创建一个p作为核心对象的新簇；
b. 寻找并合并核心对象直接密度可达的对象；
c. 没有新点可以更新簇时，算法结束。
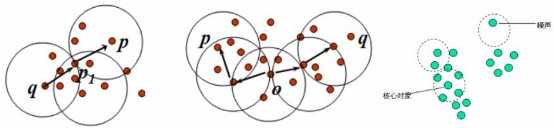
由于包含过少对象的簇被认为是噪声，这种算法的抗噪性比较好。
3、密度最大值聚类（2014年science）
算法核心：
那些有着比较大的局部密度
和很大的高密距离
的点被认为是簇的中心；
高密距离
较大但局部密度
较小的点是异常点；
确定簇中心之后，其他点按照距离已知簇的中心最近进行分类。
这种方法可以自动选择聚类中心，并且结合了DBSCAN算法的抗噪声的优点。
五、谱聚类
1、谱：
方阵作为线性算子，它的所有特征值的全体统称方阵的谱。
2、谱半径：
方阵的最大值称为谱半径。
矩阵的谱半径：
的最大特征值
3、谱聚类概述：
谱聚类是一种基于图论的聚类方法，通过对样本数据的拉普拉斯矩阵的特征向量进行聚 类，从而达到对样本数据聚类的目的。（降维）
4、未正则拉普拉斯矩阵的谱聚类算法：
输出N个点{Pi}，簇数目K。
a. 计算n×n的相似度矩阵W和度矩阵D
b. 计算拉普拉斯矩阵L=D-W
d. 令
是U的第i行的向量
e. 用k-means算法将点
聚类成簇 
f. 输出簇
5、谱聚类算法：随机游走拉普拉斯矩阵（效果最好）
a. 计算n×n的相似度矩阵W和度矩阵D
b. 计算拉普拉斯矩阵
c. 计算L的前k个特征向量
，将k个列向量
组成矩阵
d. 令
是U的第i行的向量
e. 用k-means算法将点
聚类成簇 
f. 输出簇
6、谱聚类算法：对称拉普拉斯矩
输出N个点{Pi}，簇数目K。
a. 计算n×n的相似度矩阵W和度矩阵D
b. 计算拉普拉斯矩阵
c. 计算L的前k个特征向量
，将k个列向量
组成矩阵
e. 将
依次单位化，使得
f. 用k-means算法将点
聚类成簇 
g. 输出簇
附录：拉普拉斯矩阵及其性质
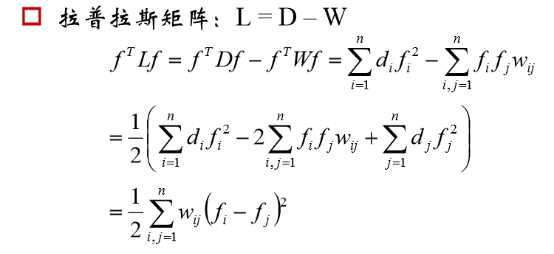
L是对称半正定矩阵，最小特征值是0，相应的特征 向量是全1向量。
五、标签传递算法
对于部分样本的标记给定，而大多数样本的标记未知的情形，是半监督学习问题。
标签传递算法(Label Propagation Algorithm,LPA)，将标记样本的标记通过一定的概率传递给未标记样本，直到最终收敛。
原文：http://www.cnblogs.com/Dr-XLJ/p/5369780.html
