这道题很有趣,采用动态规划,开始的时候,DP在我的脑海中闪过,但是没有认真去思考,后来看了前辈说采用Dp,才决定自己认真试下。
设这样一个标记数组boolean Db[0...len],Db[i]表示String[0...i]是否可segment的。当我考虑第i个字符时,应该这样想,以i为结尾的最后一个可能出现在字典里的单词的开头在哪里,才能在不破坏之前是否可segment的性质,并且可以得到真确的答案。下面是这个动态规划的递推公式:
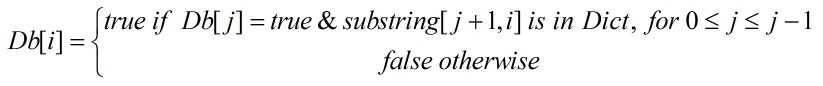
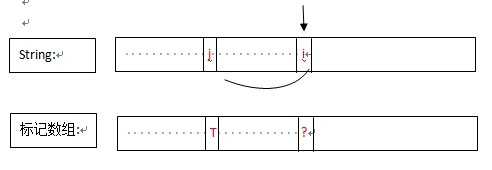
下面是已经AC的代码。
1 /** 2 * Word break 3 * Given a string s and a dictionary of words dict, 4 * determine if s can be segmented into a space-separated sequence of one or more dictionary words. 5 * 采用动态规划算法;设数组Db[0...len], Db[i]表示string[0...i]是可segmented的 6 * 采用动态规划时,很关键的一点是得弄清楚子问题是什么。 7 * 当我在考虑第i个字符时,我应该是从前面的Db[j]为true的j+1开始到i,这段字串是否在dict中,如果不再,则继续往前找合适的j(这里的合适指的是Db[j]为true) 8 * @param s 9 * @param dict 10 * @return 11 */ 12 public boolean wordBreak(String s, Set<String> dict) 13 { 14 //if the dict is empty, return false 15 if(dict.size()<=0) 16 return false; 17 boolean[] Db = new boolean[s.length()]; 18 //initialize 19 if(dict.contains(s.substring(0,1))) 20 Db[0] = true; 21 else 22 Db[0] = false; 23 //DP process 24 for(int i=1;i<s.length();i++) 25 { 26 Db[i] = false; 27 int j = i-1; 28 while(j>=0) 29 { 30 if(Db[j] && dict.contains(s.substring(j+1,i+1))) 31 { 32 Db[i] = true; 33 break; 34 } 35 j--; 36 } 37 if(!Db[i] && j<0 && dict.contains(s.substring(0,i+1))) 38 Db[i] = true; 39 40 41 } 42 return Db[s.length()-1]; 43 }
LeetCode OJ - Word Break,布布扣,bubuko.com
原文:http://www.cnblogs.com/echoht/p/3687676.html