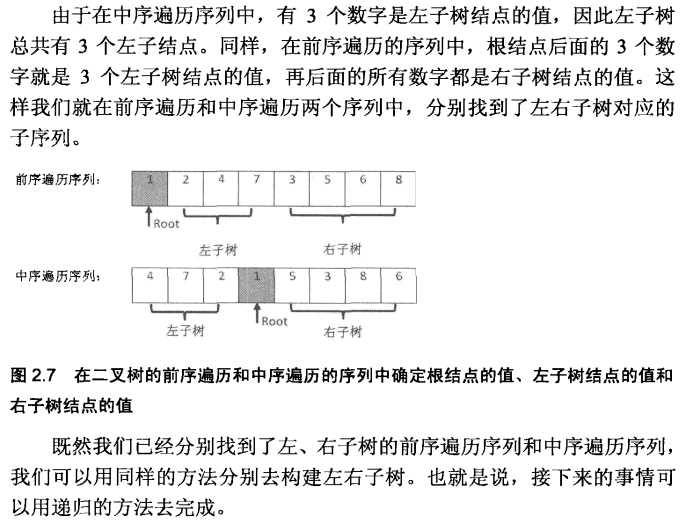
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序序列和中序序列的结果都不含重复的数字,例如输入前序序列{1,2,4,7,3,5,6,8}和中序序列{4,7,2,1,5,3,8,6},则重建树并输出它的头结点,二叉树的头结点定义如下:
struct BinaryTreeNode{
int m_value;
BinryTreeNode *pleft;
BinaryTreeNode *pright;
}
其实对于二叉树的各种遍历算法的具体实现难度远远大于理解,对我来说在上数据结构课时,就对前、中、后三种遍历思想有自认为还可以的理解(也就是说给我一棵树,我绝对可以准确的写出它的三种遍历序列,也可通过已知的前(后)序列和中序序列重新画出这棵树),但到了具体的代码实现就比较懵逼了。。。对递归这种需要在脑子中像计算机一样跑N遍的方式好难准确无误的推敲啊。。。每次遇到递归的算法就很尴尬,看的懂但是不会自己写,导致自己的动态规划算法学的很烂0.0,所以对于递归还得加强学习啊!!!
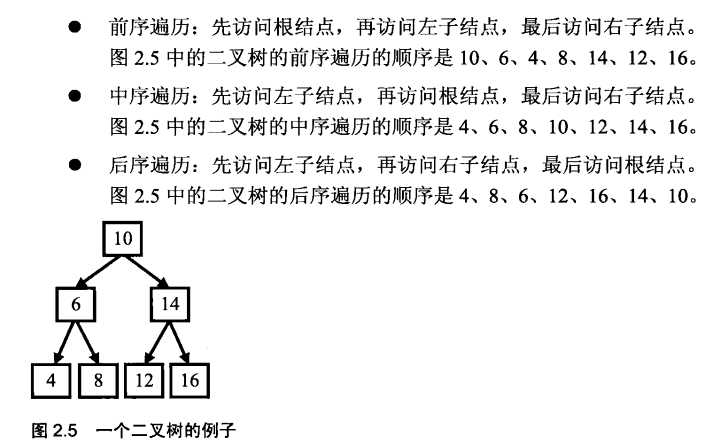
如果理解了递归的访问,那么建树的过程就容易多了,前序遍历序列的第一个数(后序遍历的最后一个数)一定是根结点,所以可以根据此结点在中序序列中的位置把中序序列分为左子树和右子数两个部分,同样的道理,在左子树和右子数中同样可以用到这样的规律来确定每个中间结点。
1 #include<iostream> 2 using namespace std; 3 struct BinaryTreeNode 4 { 5 int m_value; 6 BinaryTreeNode *p_left; 7 BinaryTreeNode *p_right; 8 }; 9 BinaryTreeNode* ConstructCore(int *startPreorder, int *endPreorder, int *startInorder, int *endInorder)//前序序列的开始、结束指针和中序序列的开始结束指针 10 { 11 int rootValue = startPreorder[0];//前序序列的第一个值必然是根结点 12 BinaryTreeNode* root = new BinaryTreeNode(); 13 root->m_value = rootValue; 14 root->p_left = nullptr; 15 root->p_right = nullptr; 16 if (startPreorder == endPreorder){ 17 if (startInorder == endInorder&&*startPreorder == *startInorder)//只有一个数字 18 return root; 19 else 20 throw exception("Invalid input"); 21 } 22 int* rootInorder = startInorder;//在中序序列中找到根节点的位置 23 while (rootInorder <= endInorder&& *rootInorder != rootValue) 24 ++rootInorder; 25 if (rootInorder == endInorder&&*rootInorder != rootValue) 26 throw exception("Invalid Input"); 27 int leftLength = rootInorder - startInorder;//左子树序列长度 28 int* leftPreorderEnd = startPreorder + leftLength;//左子树前序序列的最后一个结点 29 if (leftLength > 0)//建立左子树 30 { 31 root->p_left = ConstructCore(startPreorder + 1, leftPreorderEnd, startInorder, rootInorder-1); 32 } 33 if (leftLength < endPreorder - startPreorder)//建立右子树 34 { 35 root->p_right = ConstructCore(leftPreorderEnd + 1, endPreorder, rootInorder + 1, endInorder); 36 } 37 return root; 38 } 39 BinaryTreeNode* Construt(int *preorder, int *inorder, int length)//输入前序序列,中序序列和序列长度 40 { 41 if (preorder == nullptr || inorder == nullptr || length <= 0) 42 return nullptr; 43 return ConstructCore(preorder, preorder + length - 1, inorder, inorder + length - 1); 44 }
原文:http://www.cnblogs.com/General-up/p/5402362.html