神经网络之BP算法,梯度检验,参数随机初始化
neural network(BackPropagation algorithm,gradient checking,random initialization)
一、代价函数(cost function)
对于训练集 ,代价函数(cost
function)定义为:
,代价函数(cost
function)定义为:
其中红色方框圈起的部分为正则项,k:输出单元个数即classes个数,L:神经网络总层数, :第
:第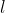 层的单元数(不包括偏置单元),
层的单元数(不包括偏置单元), :表示第
:表示第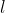 层边上的权重。
层边上的权重。
二、误差逆传播(BackPropagation,简称BP)
有了代价函数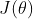 ,我们的目前显然是找到能使
,我们的目前显然是找到能使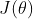 最小的参数
最小的参数 ,为了使用梯度下降或者其他优化算法,我们需要计算:
,为了使用梯度下降或者其他优化算法,我们需要计算:
 直接用上面的公式就可以求出,关键是如何计算
直接用上面的公式就可以求出,关键是如何计算 。BP算法可以求出最佳权值
。BP算法可以求出最佳权值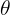 ,下面来看看BP算法的基本原理。先来看一下forward
propagation(就不画图了,直接给出Ng画的图)
,下面来看看BP算法的基本原理。先来看一下forward
propagation(就不画图了,直接给出Ng画的图)
接下来看BP算法:定义 为第L层单元i的残差。BP算法的目标是最小化
为第L层单元i的残差。BP算法的目标是最小化 。而对于样例
。而对于样例 来说,其均方误差为:
来说,其均方误差为: 。在梯度下降中,每一次迭代都按如下公式对参数
。在梯度下降中,每一次迭代都按如下公式对参数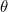 更新:
更新: 。
。
BP算法的思路如下:给定一个样例 ,先根据前向传导(forward propagation)计算出神经网络中的所有激活值。针对第
,先根据前向传导(forward propagation)计算出神经网络中的所有激活值。针对第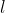 层的每一个节点i,我们可以计算出其“残差”
层的每一个节点i,我们可以计算出其“残差” ,该残差表明了该节点对最终输出值的残差产生了多少影响。对于最后一层输出层,我们可以直接计算出神经网络的输出
,该残差表明了该节点对最终输出值的残差产生了多少影响。对于最后一层输出层,我们可以直接计算出神经网络的输出 与实际类别值之间的残差。那么重点是对于隐藏层该如何处理?我们将基于节点第
与实际类别值之间的残差。那么重点是对于隐藏层该如何处理?我们将基于节点第 层的残差的加权平均值计算出
层的残差的加权平均值计算出 ,这些节点以
,这些节点以 作为输入。
作为输入。
因此,对于最后一层输出层L(用L表示最后一层输出层)来说:
对于隐藏层 来说:
来说:
因此可得:
这样,我们就可以求得偏导数: ,因此
,因此 。
。
关于BP算法的公式推导已经介绍完了,大家可以自己在纸上推导一下。下面来总结一下,BP算法的执行过程(直接盗用ng的图吧):
以上就是BP算法的细节原理。概括来讲就是:
1、利用forward propagation计算出每一层的“激活值” 。
。
2、计算出最后一层即输出层每个输出单元的残差 。
。
4、计算出我们需要的偏导数。
讲了这么多,大家来看看NG举得例子,可行更加形象化的让大家体会下BP算法的执行过程细节:
三、梯度检验(gradient checking)
BP算法细节繁多,而且甚是复杂,因此非常容易出错,很难检查出来。因此需要使用梯度检验,梯度检验能够非常的确信的检验你实现的BP算法是否正确。梯度检验如下图所示(图片来自ng machine learning 课):
因此,对于每个参数 使用梯度检验:
使用梯度检验:
因为在BP算法执行过程中,我们就可以将这个近似值与 的导数相比较,如果两者相同或者非常接近,则可以确认我们实现的BP算法是正确的。有个注意点:当你训练BP神经网络时,一定要关闭gradient checking,因为梯度检验的执行速度非常非常慢。
的导数相比较,如果两者相同或者非常接近,则可以确认我们实现的BP算法是正确的。有个注意点:当你训练BP神经网络时,一定要关闭gradient checking,因为梯度检验的执行速度非常非常慢。
四、参数随机初始化(random initialization)
我们在线性回归和logistic回归中都可以把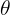 初始化为zeros(n,1),这样做是可以的。但是在神经网络中这样做却是不可以的,因为如果初始化的参数一样,意味着隐藏层的每个单元的输入权重是一样的,因此每次更新后隐藏层的单元值将会是一样的。这就意味着所有的隐藏层单元都在计算相同的特征,这是完全多余的。来个图形象化的理解一下:
初始化为zeros(n,1),这样做是可以的。但是在神经网络中这样做却是不可以的,因为如果初始化的参数一样,意味着隐藏层的每个单元的输入权重是一样的,因此每次更新后隐藏层的单元值将会是一样的。这就意味着所有的隐藏层单元都在计算相同的特征,这是完全多余的。来个图形象化的理解一下:
因为在神经网络参数(权重)初始化的时候,需要随机初始化,就是把 的值随机初始化,范围为
的值随机初始化,范围为 。
。
注:提供一些参考资料给大家,能够更好的帮助大家更好的理解神经网络。
神经网络详解 Detailed neural network
原文:http://blog.csdn.net/u012328159/article/details/51168939







