题意:给出A,B, C点坐标求D,E,F坐标,其中每个角都被均等分成三份 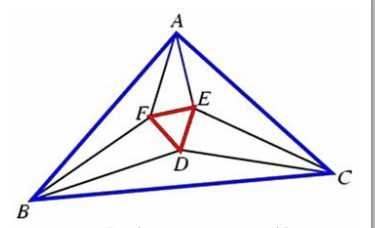
求出 ABC的角a, 由 BC 逆时针旋转 a/3 得到BD,然后 求出 ACB 的角a2, 然后 由 BC顺时针 旋转 a2 / 3得到 DC,然后就交点

1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cstring> 5 #include <cmath> 6 using namespace std; 7 struct Point 8 { 9 double x, y; 10 }; 11 typedef Point Vector; 12 Vector operator + (Vector A, Vector B) 13 { 14 Vector C; 15 C.x = A.x + B.x; 16 C.y = A.y + B.y; 17 return C; 18 } 19 Vector operator - (Vector A, Vector B) 20 { 21 Vector C; 22 C.x = A.x - B.x; 23 C.y = A.y - B.y; 24 return C; 25 } 26 Vector operator *(Vector A, double b) 27 { 28 Vector C; 29 C.x = A.x * b; 30 C.y = A.y * b; 31 return C; 32 } 33 Point read_point() 34 { 35 Point temp; 36 scanf("%lf%lf", &temp.x, &temp.y); 37 return temp; 38 } 39 double Dot(Vector A, Vector B) 40 { 41 return A.x * B.x + A.y * B.y; 42 } 43 double Length(Vector A) 44 { 45 return sqrt(Dot(A, A)); 46 } 47 double Angle(Vector A, Vector B) 48 { 49 return acos(Dot(A, B) / Length(A) / Length(B)); 50 } 51 Vector Rotate(Vector A, double rad) 52 { 53 Vector C; 54 C.x = A.x * cos(rad) - A.y * sin(rad); 55 C.y = A.x * sin(rad) + A.y * cos(rad); 56 return C; 57 } 58 double Cross(Vector A, Vector B) 59 { 60 return A.x * B.y - A.y * B.x; 61 } 62 Point GetLineIntersection(Point P, Vector v, Point Q, Vector w) 63 { 64 Vector u = P - Q; 65 double t = Cross(w, u) / Cross(v, w); 66 return P + v * t; 67 } 68 Point getD(Point A, Point B, Point C) 69 { 70 Vector v1 = C - B; 71 double a1 = Angle(A - B, v1); 72 v1 = Rotate(v1, a1 / 3); 73 74 Vector v2 = B - C; 75 double a2 = Angle(A - C, v2); 76 v2 = Rotate(v2, -a2 / 3); 77 78 return GetLineIntersection(B, v1, C, v2); 79 80 } 81 int main() 82 { 83 int T; 84 Point A, B, C, D, E, F; 85 scanf("%d", &T); 86 while (T--) 87 { 88 A = read_point(); 89 B = read_point(); 90 C = read_point(); 91 D = getD(A, B, C); 92 E = getD(B, C, A); 93 F = getD(C, A, B); 94 95 printf("%.6lf %.6lf %.6lf %.6lf %.6lf %.6lf\n", D.x, D.y, E.x, E.y, F.x, F.y); 96 97 } 98 return 0; 99 }
UVA11178 Morley's Theorem(基础模板)
原文:http://www.cnblogs.com/zhaopAC/p/5413469.html