炮兵阵地
Description
司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成,地图的每一格可能是山地(用"H" 表示),也可能是平原(用"P"表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
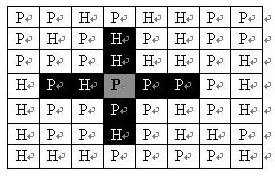
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
Input
第一行包含两个由空格分割开的正整数,分别表示N和M;
接下来的N行,每一行含有连续的M个字符(‘P‘或者‘H‘),中间没有空格。按顺序表示地图中每一行的数据。N <= 100;M <= 10。
Output
仅一行,包含一个整数K,表示最多能摆放的炮兵部队的数量。
Sample Input
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
Sample Output
6
Source
Noi 01
【分析】
首先,这种题目一看就知道要用DP(看不出来的再去修炼。。。)
但是,如果我们枚举每个位置的状态的话,最坏情况下需要枚举2mn次,即时间复杂度是O(2mn),瞄一瞄m和n,就发现mn≤1000,如果暴力的话,呵呵。
再仔细一看,咦?怎么m这么小?那么,我们可以将每一行当作一个状态,它的数值换成二进制后,对应的位为1则表示放了炮兵,否则没放。例如,某行的状态是66,其二进制为1000010,则表明该行第1个位置和第6个位置放了炮兵。由于m≤10,所以每一行的总状态数≤210=1024,嗯,明显比暴力优。
再仔细瞄一瞄,状态数真的有1024种那么多吗?答案是:Of course……not.对于一些状态,如(67)10=(1000011)2是不合法的,因为第6个炮兵会和第7个炮兵掐起来。所以,我们可以离线算出合法的方案数,结果发现,只有60种!(OMG!)
当然,接下来就到了核心部分了——DP方程。
由于炮兵攻击范围是两格,所以两个参数(一个表示第几行,另一个表示状态)肯定是不行的,因为这样无法保证上两行的炮兵不跟当前行的炮兵掐起来。所以,我们考虑用三个参数。
设F[i,j,k]表示第i行状态为j,第i-1行状态为k时1~i行能放的最大炮兵数。则有F[i,j,k]=F[i-1,k,L]+num[j],其中num[j]表示j状态中放置炮兵的总数。
因为第1行的状态是独立的,所以我们可以先暴力求出第1行的所有状态。(这里暴力才60……)
又因为第2行只与第1行有关,所以我们又可以暴力求出第2行的所有状态。(这里暴力最坏才602=3600……)
然后,枚举i、j、k、L,一直算下去就ok了。最后取F[n]中所有值的最大值即可。
【AC代码如下】
program gun; const //所有状态 state:array[1..60]of longint =(0,1,2,4,8,9,16,17,18,32,33,34,36,64,65, 66,68,72,73,128,129,130,132,136,137,144,145,146,256,257, 258,260,264,265,272,273,274,288,289,290,292,512,513,514,516, 520,521,528,529,530,544,545,546,548,576,577,578,580,584,585); //每种状态对应的炮兵数 num:array[1..60]of longint =(0,1,1,1,1,2,1,2,2,1,2,2,2,1,2, 2,2,2,3,1,2,2,2,2,3,2,3,3,1,2, 2,2,2,3,2,3,3,2,3,3,3,1,2,2,2, 2,3,2,3,3,2,3,3,3,2,3,3,3,3,4); var n,m,i,j,k,l,ans,maximum:longint; map:array[1..100]of longint; f:array[1..100,1..60,1..60]of longint; procedure readin; var i,j:longint; c:char; begin readln(n,m); for i:= 1 to n do begin map[i]:=0; for j:= 1 to m do begin read(c); if c=‘P‘ then map[i]:=map[i] or (1 shl (m-j)); //读图时直接把图压缩 end; readln; end; j:=1 shl m-1; maximum:=0; for i:= 1 to 60 do if state[i]>j then begin maximum:=i-1; break; end; if maximum=0 then maximum:=i; //统计二进制位长度为m的状态总数 end; procedure init; var i,j:longint; begin //预处理出第1行的所有状态 for i:= 1 to maximum do if state[i] or map[1]=map[1] then f[1,i,1]:=num[i]; //预处理出第2行的所有状态 for i:= 1 to maximum do if state[i] or map[2]=map[2] then begin for j:= 1 to maximum do if (state[j] or map[1]=map[1]) and (state[i] and state[j]=0) then f[2,i,j]:=f[1,j,1]+num[i]; end; end; function max(a,b:longint):longint; begin if a>b then exit(a) else exit(b); end; begin readin; init; for i:= 3 to n do begin for j:= 1 to maximum do if state[j] or map[i]=map[i] then //这里用or是因为:如果枚举的状态不符合地形的要求,肯定会在二进制中多出几个1,这样就和地图不相等了 begin for k:= 1 to maximum do if (state[k] or map[i-1]=map[i-1]) and (state[j] and state[k]=0) then //这里用and是因为:如果两个状态and运算后不为0,那么就一定有两个炮兵在相同位置,这样他们就会掐起来,与题意不符 begin for l:= 1 to maximum do if (state[l] or map[i-2]=map[i-2]) and (state[j] and state[l]=0) and (state[k] and state[l]=0) then begin f[i,j,k]:=max(f[i,j,k],f[i-1,k,l]+num[j]); end; end; end; end; ans:=0; //寻找F[n]中的最大值 if n>0 then begin for i:= 1 to maximum do for j:= 1 to maximum do if f[n,i,j]>ans then ans:=f[n,i,j]; end; writeln(ans); end.
原文:http://www.cnblogs.com/bigTG/p/3690388.html