http://poj.org/problem?id=1066
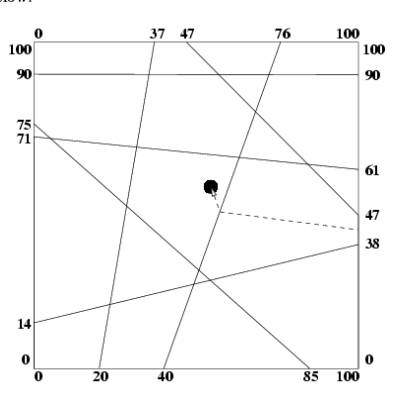
题意:给出一个100*100的正方形区域,通过若干连接区域边界的线段将正方形区域分割为多个不规则多边形小区域,然后给出宝藏位置,要求从区域外部开辟到宝藏所在位置的一条路径,使得开辟路径所需要打通的墙壁数最少("打通一堵墙"即在墙壁所在线段中间位置开一空间以连通外界),输出应打通墙壁的个数(包括边界上墙壁)。
思路:用结构体保存中点,然后判断这些点之间能否连通,最短路即可
由于精度问题,在判断线段相交时精度没有处理好导致答案一直不对,debug了两天都不知道是因为这,最后学长帮忙看出了是精度问题,当A掉的那一刻,我整个人都好了
#include <iostream>
#include <stdio.h>
#include <cstring>
#include <cmath>
#include <queue>
#include <algorithm>
using namespace std;
typedef long long LL;
#define N 1500
#define INF 0x3f3f3f3f
#define met(a, b) memset (a, b, sizeof(a))
const double EPS = 1e-6;
struct point
{
double x, y;
} MidPoint[N];
struct Line1
{
point a, b;
point p[N];
int k;
} Line[40];
int n, g[N][N], vis[N], dist[N];
bool cmp (point a, point b)
{
///对一条线段上的交点进行从左到右的排序
if (fabs(a.x-b.x) > EPS) return a.x < b.x;
return a.y < b.y;
}
double xmult (point p1, point p2, point p0)
{
return (p1.x-p0.x)*(p2.y-p0.y) - (p2.x-p0.x)*(p1.y-p0.y);
}
bool IsParallel (point s1, point e1, point s2, point e2)
{
///判断两线段是否平行
if (fabs ((e1.y-s1.y)*(e2.x-s2.x) - (e1.x-s1.x)*(e2.y-s2.y)) < EPS) return true;
return false;
}
bool IsIntersected (point s1, point e1, point s2, point e2)///判断两线段相交
{
return (max (s1.x, e1.x) >= min (s2.x, e2.x)) &&
(max (s2.x, e2.x) >= min (s1.x, e1.x)) &&
(max (s1.y, e1.y) >= min (s2.y, e2.y)) &&
(max (s2.y, e2.y) >= min (s1.y, e1.y)) &&
(xmult (s1, s2, e1) * xmult (s1, e1, e2) > EPS) &&
(xmult (s2, s1, e2) * xmult (s2, e2, e1) > EPS);
}
point InterSection (point s1, point e1, point s2, point e2)
{
///求两线段交点
point ret = s1;
double t = ((s1.x-s2.x)*(s2.y-e2.y) - (s1.y-s2.y)*(s2.x-e2.x))
/((s1.x-e1.x)*(s2.y-e2.y) - (s1.y-e1.y)*(s2.x-e2.x));
ret.x += (e1.x-s1.x) * t;
ret.y += (e1.y-s1.y) * t;
return ret;
}
void IsGet (int m)///判断两点之间是否可达
{
for (int i=0; i<=m; i++)
for (int j=0; j<=m; j++)
{
///初始化
if (i == j) g[i][j] = 0;
else g[i][j] = INF;
}
for (int i=0; i<m; i++)
{
for (int j=i+1; j<m; j++)
{
int flag = 0;
for (int k=1; k<=n; k++)
{///遍历所有的线段
double x1 = Line[k].a.x, y1 = Line[k].a.y;
double x2 = Line[k].b.x, y2 = Line[k].b.y;
if (IsIntersected (MidPoint[i], MidPoint[j], Line[k].a, Line[k].b))///两点之间不可达
{
flag = 1;
break;
}
}
if (!flag) g[i][j] = g[j][i] = 1;
}
}
}
void CunChujiaodian ()///存储该条线段和其他所有线段的交点
{
for (int i=1; i<=n; i++)
{
int k = 0;
if (i==n-3 || i==n)
{
for (int j=1; j<=n; j++)
{
if (i == j) continue;
if (fabs(Line[j].a.y-Line[i].a.y)<EPS)
{
Line[i].p[k].x = Line[j].a.x;
Line[i].p[k].y = Line[j].a.y;
k++;
}
if (fabs(Line[j].b.y-Line[i].a.y)<EPS)
{
Line[i].p[k].x = Line[j].b.x;
Line[i].p[k].y = Line[j].b.y;
k++;
}
}
Line[i].k = k;
}
else if (i==n-2 || i==n-1)
{
for (int j=1; j<=n; j++)
{
if (i == j) continue;
if (fabs(Line[j].a.x-Line[i].a.x)<EPS)
{
Line[i].p[k].x = Line[j].a.x;
Line[i].p[k++].y = Line[j].a.y;
}
if (fabs(Line[j].b.x-Line[i].a.x)<EPS)
{
Line[i].p[k].x = Line[j].b.x;
Line[i].p[k++].y = Line[j].b.y;
}
}
Line[i].k = k;
}
else///其他情况
{
for (int j=1; j<=n; j++)
{
if (i == j) continue;
if (!IsParallel (Line[i].a, Line[i].b, Line[j].a, Line[j].b))///两条线段不平行
if (IsIntersected (Line[i].a, Line[i].b, Line[j].a, Line[j].b))///两条线段相交
{
point ret = InterSection (Line[i].a, Line[i].b, Line[j].a, Line[j].b);
///存储该条线段和其他所有线段的交点
Line[i].p[k].x = ret.x;
Line[i].p[k++].y = ret.y;
}
}
Line[i].p[k].x = Line[i].a.x;
Line[i].p[k++].y = Line[i].a.y;
Line[i].p[k].x = Line[i].b.x;
Line[i].p[k++].y = Line[i].b.y;
Line[i].k = k;
}
}
}
void Dij (int sa, int m)///最短路
{
met (vis, 0);
for (int i=0; i<m; i++)
dist[i] = g[sa][i];
vis[0] = 1;
dist[0] = 0;
for (int i=0; i<m; i++)
{
int minx = INF, Index = 0;
for (int j=0; j<m; j++)
if (!vis[j] && dist[j] < minx)
minx = dist[Index = j];
vis[Index] = 1;
for (int j=0; j<m; j++)
if (!vis[j] && dist[j] > dist[Index] + g[Index][j])
dist[j] = dist[Index] + g[Index][j];
}
int minx = INF;
for (int i=0; i<m; i++)
{
if (MidPoint[i].x<EPS || fabs(MidPoint[i].x-100)<EPS || MidPoint[i].y<EPS || fabs(MidPoint[i].y-100)<EPS)
minx = min (minx, dist[i]);///找到最少需要炸开的门
}
printf ("Number of doors = %d\n", minx);
}
void Solve ()
{
CunChujiaodian();///存储该条线段和其他所有线段的交点
int k = 1;
for (int i=1; i<=n; i++)
{
sort (Line[i].p, Line[i].p+Line[i].k, cmp);
for (int j=1; j<Line[i].k; j++)
{
///计算所以的中的坐标保存在数组MidPoint中
MidPoint[k].x = (Line[i].p[j-1].x+Line[i].p[j].x) / 2;
MidPoint[k++].y = (Line[i].p[j-1].y+Line[i].p[j].y) / 2;
}
}
IsGet (k);///判断两点之间是否可达
Dij (0, k);
}
int main ()
{
while (scanf ("%d", &n) != EOF)
{
met (Line, 0);
met (MidPoint, 0);
for (int i=1; i<=n; i++)
scanf ("%lf%lf%lf%lf", &Line[i].a.x, &Line[i].a.y, &Line[i].b.x, &Line[i].b.y);
double x, y;
scanf ("%lf%lf", &x, &y);
MidPoint[0].x = x, MidPoint[0].y = y;///起始位置(宝藏位置)
Line[n+1].a.x = 0, Line[n+1].a.y = 0, Line[n+1].b.x = 100, Line[n+1].b.y = 0;
Line[n+2].a.x = 0, Line[n+2].a.y = 0, Line[n+2].b.x = 0, Line[n+2].b.y = 100;
Line[n+3].a.x = 100, Line[n+3].a.y = 0, Line[n+3].b.x = 100, Line[n+3].b.y = 100;
Line[n+4].a.x = 0, Line[n+4].a.y = 100, Line[n+4].b.x = 100, Line[n+4].b.y = 100;
///边缘的四条线段
n += 4;
Solve ();
}
return 0;
}


原文:http://blog.csdn.net/w144215160044/article/details/51263585