The
Head Elder of the tropical island of Lagrishan has a problem. A burst
of foreign aid money was spent on extra roads between villages some
years ago. But the jungle overtakes roads relentlessly, so the large
road network is too expensive to maintain. The Council of Elders must
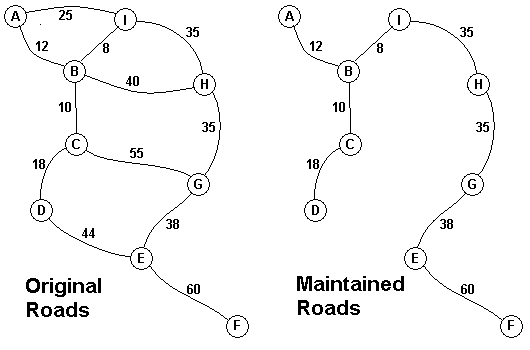
choose to stop maintaining some roads. The map above on the left shows
all the roads in use now and the cost in aacms per month to maintain
them. Of course there needs to be some way to get between all the
villages on maintained roads, even if the route is not as short as
before. The Chief Elder would like to tell the Council of Elders what
would be the smallest amount they could spend in aacms per month to
maintain roads that would connect all the villages. The villages are
labeled A through I in the maps above. The map on the right shows the
roads that could be maintained most cheaply, for 216 aacms per month.
Your task is to write a program that will solve such problems.
The
input consists of one to 100 data sets, followed by a final line
containing only 0. Each data set starts with a line containing only a
number n, which is the number of villages, 1 < n < 27, and the
villages are labeled with the first n letters of the alphabet,
capitalized. Each data set is completed with n-1 lines that start with
village labels in alphabetical order. There is no line for the last
village. Each line for a village starts with the village label followed
by a number, k, of roads from this village to villages with labels later
in the alphabet. If k is greater than 0, the line continues with data
for each of the k roads. The data for each road is the village label for
the other end of the road followed by the monthly maintenance cost in
aacms for the road. Maintenance costs will be positive integers less
than 100. All data fields in the row are separated by single blanks. The
road network will always allow travel between all the villages. The
network will never have more than 75 roads. No village will have more
than 15 roads going to other villages (before or after in the alphabet).
In the sample input below, the first data set goes with the map above.
The
output is one integer per line for each data set: the minimum cost in
aacms per month to maintain a road system that connect all the villages.
Caution: A brute force solution that examines every possible set of
roads will not finish within the one minute time limit.
9
A 2 B 12 I 25
B 3 C 10 H 40 I 8
C 2 D 18 G 55
D 1 E 44
E 2 F 60 G 38
F 0
G 1 H 35
H 1 I 35
3
A 2 B 10 C 40
B 1 C 20
0
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
using namespace std;
const int N = 30;
const int M = 3000;
struct Edge{
int s,e,len;
}edge[M];
int father[N],n;
int _find(int x){
if(x==father[x]) return x;
return _find(father[x]);
}
int cmp(Edge a,Edge b){
return a.len<b.len;
}
int kruskal(int m){
sort(edge+1,edge+m+1,cmp);
int cost = 0;
for(int i=1;i<=m;i++){
int x = _find(edge[i].s);
int y = _find(edge[i].e);
if(x!=y){
father[x] = y;
cost+=edge[i].len;
}
}
return cost;
}
int main(){
while(~scanf("%d",&n),n){
for(int i=0;i<n;i++) father[i] = i;
int m = 1;
for(int i=1;i<n;i++){
char c[2],c1[2];
int k,len;
scanf("%s%d",c,&k);
while(k--){
scanf("%s%d",c1,&len);
edge[m].s = c[0]-‘A‘;
edge[m].e = c1[0]-‘A‘;
edge[m++].len = len;
}
}
m--;
printf("%d\n",kruskal(m));
}
}
