对于包含N个数的输入数组来说,快速排序是一种最坏情况时间复杂度为O(n2)的排序算法。虽然最坏情况时间复杂度很差,但是快速排序通常是实际排序应用中最好的选择,因为它的平均性能非常好:它的期望时间复杂度是O(nlgn),而且O(nlgn)中的隐藏因子非常小。另外,它还能够进行原址重排,甚至在虚存环境中也能很好地工作。
对数组A[p..r]进行快速排序的三步分治过程:
分解
数组A[p..r]被划分为两个(可能为空)子数组A[p..q-1]和A[q+1..r]。其中使得数组A[p..q-1]中的每个元素都小于等于A[q],而A[q]小于等于数组A[q+1..r]中的每个元素。
计算下标q也是划分过程的部分
解决
通过递归调用快速排序,对于数组A[p..q-1]和A[q+1..r]进行排序
合并
因为子数组都是原址排序,所以不需要合并操作,数组A[p..r]已经有序
下面给出快速排序实现的伪代码
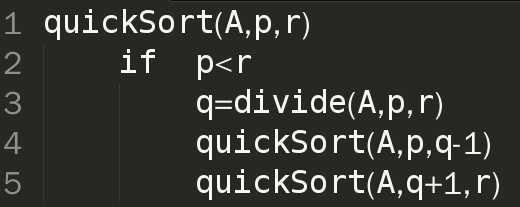
为了排序一个数组A的全部元素,初始调用是quickSort(A,1,A.length).
第3步是很重要的一步,它实现了对子数组的原址重排,可以有很多实现方法,下面给出一种,伪代码为:

下面给出示例代码

1 package codeforgod; 2 3 /** 4 * @author gejing gjblmdlm@sina.com 5 * @version 创建时间:2014年4月28日 下午6:25:09 类说明 :快速排序 6 */ 7 public class QuickSortDemo { 8 9 public void quickSort(int a[], int p, int r) { 10 if (p < r) { // 需要继续排序 11 int q = divide(a, p, r); 12 quickSort(a, p, q - 1); 13 quickSort(a, q + 1, r); 14 } 15 16 } 17 18 /** 19 * 对数组进行原址重排 20 * 21 * @param a 22 * @param p 23 * @param r 24 * @return 划分位置q 25 */ 26 private int divide(int[] a, int p, int r) { 27 int x = a[r]; 28 int i = p - 1; 29 int temp = 0; 30 for (int j = p; j <= r - 1; j++) { 31 if (a[j] <= x) { 32 i++; 33 temp = a[i]; 34 a[i] = a[j]; 35 a[j] = temp; 36 } 37 } 38 temp = a[i + 1]; 39 a[i + 1] = a[r]; 40 a[r] = temp; 41 return i + 1; 42 } 43 44 public static void main(String[] args) { 45 QuickSortDemo qs = new QuickSortDemo(); // 实例化一个对象 46 int A[] = { 5, 9, 13, 6, 2, 7, 30, 23, 17, 10 }; 47 System.out.print("原始序列: "); 48 for (int i : A) { 49 System.out.print(i + "\t"); 50 } 51 qs.quickSort(A, 0, A.length - 1); // 调用方法进行排序 52 System.out.println(); 53 System.out.print("快排之后: "); 54 for (int i : A) { 55 System.out.print(i + "\t"); 56 } 57 58 } 59 60 }
原文:http://www.cnblogs.com/blmdlm/p/3697042.html