#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;

int index[1005];
int dp[1005];
int ans[1005];

struct node
{
    int a;
    int b;
    int pos;
}nod[1005];

int cmp(node p1,node p2)
{
    if(p1.a<p2.a) return 1;
    //if(p1.b>p2.b) return 1;
    return 0;
}

void debug()
{
    int i;
    cout<<"******"<<endl;
    for(i=0;i<9;i++)
        cout<<nod[i].a<<" "<<nod[i].b<<" "<<nod[i].pos<<endl;
    cout<<"#######"<<endl;
}

int main()
{
    int n=0;

    int p1,p2;
    int i,j;
    while(cin>>p1>>p2)
    {
        nod[n].a=p1;
        nod[n].b=p2;
        nod[n].pos=n+1;
        n++;
    }

    sort(nod,nod+n,cmp);
    //memset(dp,1,sizeof(dp));
    //debug();
    for(i=0;i<=1000;i++)
    {
        dp[i]=1;
        index[i]=0;
    }

    int tmp,ma=1;
    for(i=0;i<n;i++)
        for(j=i+1;j<n;j++)
        {
            if(nod[i].a<nod[j].a&&nod[i].b>nod[j].b)
            {
                if(dp[i]+1>dp[j])
                {
                    dp[j]=dp[i]+1;
                    if(dp[j]>ma)
                    {
                        ma=dp[j];
                        tmp=j;
                    }
                    index[j]=i;
                }
            }
        }

    //cout<<ma<<endl;
    int k=0;
    while(tmp)
    {
        ans[k++]=nod[tmp].pos;
        tmp=index[tmp];
    }

    cout<<k<<endl;
    for(i=k-1;i>=0;i--)
        cout<<ans[i]<<endl;

    return 0;
}

/*
6008 1300
6000 2100
500 2000
1000 4000
1100 3000
6000 2000
8000 1400
6000 1200
2000 1900
*/

Constructing Roads In JGShining‘s Kingdom

JGShining‘s kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.

Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource. You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource. 

With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they‘re unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor cities don‘t wanna build a road with other poor ones, and rich ones also can‘t abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.

Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II. 

The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones. 

But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.

For example, the roads in Figure I are forbidden.



In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^

2
1 2
2 1
3
1 2
2 3
3 1

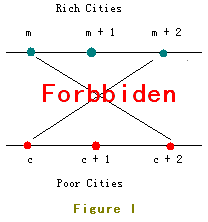
Case 1:
My king, at most 1 road can be built.

Case 2:
My king, at most 2 roads can be built.

Hint
Huge input, scanf is recommended.
 

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

struct node
{
    int x;
    int y;
}nod[500005];

int ans[500005];

int cmp(node a,node b)
{
    return a.x<b.x;
}

int main()
{
    int cas=0;
    int n,i;
    while(cin>>n)
    {
        for(i=0;i<n;i++)
            scanf("%d%d",&nod[i].x,&nod[i].y);

        sort(nod,nod+n,cmp);
        for(i=1;i<=5e5;i++)
            ans[i]=1e6;

        for(i=0;i<n;i++)
        {
            int x=nod[i].y;
            int l=0,r=5e5,mid;
            while(r>l+1)
            {
                mid=(l+r)>>1;
                if(ans[mid]<x) l=mid;
                else r=mid;
            }
            ans[l+1]=x;
        }

        int res;
        for(i=5e5;i>=1;i--)
            if(ans[i]<1e6)
            {
                res=i;
                break;
            }

        printf("Case %d:\n",++cas);
        if(res>1)
            printf("My king, at most %d roads can be built.\n\n",res);
        else
            printf("My king, at most %d road can be built.\n\n",res);
    }
    return 0;
}

/*
2
1 2
2 1
3
1 2
2 3
3 1
5
2 2
3 3
4 1
1 4
5 5
*/