在程序设计竞赛中,我们时常会遇到序列求最值的问题。在讲今天的问题之前,先小小的说明一下,子序列与子串的问题。
子序列:在原序列中不一定连续;
子串:在原序列中必须连续。
接下来,就开始今天要讲的最长公共子序列LCS(Longest Common Subsequence).对于LCS这一类的问题,一般是相对于两个序列而言,str[]与ch[]。先假设str的长度为n,ch的长度为m。假设str[]="ASBDAH",ch[]="SDAAH";其中"SDA"是其中的str与ch的一个子序列,但不是最长的。最长的子序列为"SDAH",当然,有时候我们会看到两个串中有多个相同长度的子序列,这不足为奇。
如果我们枚举str的子序列,那么将有2n个子序列,这很不切实际。因此我们可以试着让str中前1,2,3……n参与的情况下分别与ch串中前1,2……m参与情况求出LCS。
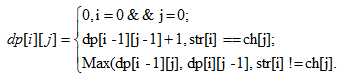
dp[i][j]表示str前i个参与,以及ch前j个参与的LCS。
当str[i] == ch[j]时,只需要记录统计出str[1~i - 1],ch[1~j - 1]的LCS,在此基础上加1.
当str[i] != ch[j]时,我们只需要求str[1 ~ i - 1]且ch[1~j],str[1 ~ i]且ch[1~j-1]的最大值即可。

1 #include <iostream> 2 #include <string.h> 3 #include <stdio.h> 4 #include <math.h> 5 using namespace std; 6 const int MAX = 100 + 10; 7 char str[MAX], ch[MAX]; 8 int dp[MAX][MAX]; 9 10 int max(int a, int b){ return a > b ? a : b;} 11 12 int main() 13 { 14 int t, n, m; 15 scanf("%d", &t); 16 getchar(); 17 18 while (t--) 19 { 20 scanf("%s%s", str, ch); 21 n = strlen(str); 22 m = strlen(ch); 23 24 for (int i = 0; i < n; i++) 25 { 26 for (int j = 0; j < m; j++) 27 { 28 if (str[i] == ch[j]) 29 { 30 dp[i + 1][j + 1] = dp[i][j] + 1; 31 } 32 else dp[i + 1][j + 1] = max(dp[i + 1][j], dp[i][j + 1]); 33 } 34 } 35 36 printf("%d\n", dp[n][m]); 37 38 } 39 40 return 0; 41 }
序列最的问题之最长公共子序列LCS,布布扣,bubuko.com
原文:http://www.cnblogs.com/1949yang/p/3701104.html