题目链接:
http://poj.org/problem?id=1707
|
Language:
Sum of powers
Description
A young schoolboy would like to calculate the sum
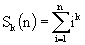 for some fixed natural k and different natural n. He observed that calculating ik for all i (1<=i<=n) and summing up results is a too slow way to do it, because the number of required arithmetical operations increases as n increases. Fortunately, there is another method which takes only a constant number of operations regardless of n. It is possible to show that the sum Sk(n) is equal to some polynomial of degree k+1 in the variable n with rational coefficients, i.e., 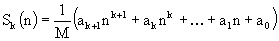 We require that integer M be positive and as small as possible. Under this condition the entire set of such numbers (i.e. M, ak+1, ak, ... , a1, a0) will be unique for the given k. You have to write a program to find such set of coefficients to help the schoolboy make his calculations quicker. Input
The input file contains a single integer k (1<=k<=20).
Output
Write integer numbers M, ak+1, ak, ... , a1, a0 to the output file in the given order. Numbers should be separated by one space. Remember that you should write the answer with the smallest positive M possible.
Sample Input 2 Sample Output 6 2 3 1 0 Source |
题目意思:
已知

解题思路:
伯努利数:http://zh.wikipedia.org/wiki/%E4%BC%AF%E5%8A%AA%E5%88%A9%E6%95%B0
所以有1^k+2^k+3^k+...+n^k=1/(k+1)(C[k+1,0)*B[0]*n^(k+1-0)+C[k+1,1]*B[1]*n^(k+1-1)+...+C[k+1,j]*B[j]*n^(k+1-j)+...+C[k+1,k]*B[k]*n^(k+1-k))+n^k
先求出伯努利数,然后分母求最小公倍数即可。
注意n^k的系数要加上后面的n^k为C[k+1,1]*B[1]+(k+1)
最后只剩下分数加法了。注意最大公约数为负数的情况,强制转化为正数,用分子保存整个分数的正负性。
代码:
//#include<CSpreadSheet.h>
#include<iostream>
#include<cmath>
#include<cstdio>
#include<sstream>
#include<cstdlib>
#include<string>
#include<string.h>
#include<cstring>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<stack>
#include<list>
#include<queue>
#include<ctime>
#include<bitset>
#include<cmath>
#define eps 1e-6
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define ll __int64
#define LL long long
#define lson l,m,(rt<<1)
#define rson m+1,r,(rt<<1)|1
#define M 1000000007
//#pragma comment(linker, "/STACK:1024000000,1024000000")
using namespace std;
#define Maxn 25
ll C[Maxn][Maxn];
struct PP
{
ll a,b;
}B[Maxn],ans[Maxn];
ll k;
ll gcd(ll a,ll b)
{
if(a%b==0)
{
if(b>0)
return b;
return -b;
}
return gcd(b,a%b);
}
PP add(PP a,PP b) //模拟两个分数的加法
{
if(!a.a) //如果有一个为0
return b;
if(!b.a)
return a;
ll temp=a.b/gcd(a.b,b.b)*b.b; //求出分母的最小公倍数
//printf("%I64d\n",temp);
PP res;
res.a=temp/a.b*a.a+temp/b.b*b.a; //分子相加
res.b=temp;
if(res.a) //约掉最大公约数
{
ll tt=gcd(res.a,res.b);
res.b/=tt;
res.a/=tt;
}
return res;
}
void init()
{
memset(C,0,sizeof(C));
for(int i=0;i<=25;i++)
{
C[i][0]=1;
for(int j=1;j<i;j++)
C[i][j]=C[i-1][j]+C[i-1][j-1];
C[i][i]=1;
}
B[0].a=1,B[0].b=1; //求伯努利数
for(int i=1;i<=20;i++) //用递推关系求
{
PP temp;
temp.a=0;
temp.b=0;
for(int j=0;j<i;j++)
{
PP tt=B[j];
tt.a=tt.a*C[i+1][j];
//printf("::::%I64d %I64d:\n",tt.a,tt.b);
if(tt.a)
{
ll te=gcd(tt.a,tt.b);
tt.a/=te;
tt.b/=te;
}
temp=add(temp,tt);
//printf("i:%d j:%d %I64d %I64d:\n",i,j,temp.a,temp.b);
//system("pause");
}
temp.a=-temp.a;
temp.b*=C[i+1][i];
//printf("%I64d %I64d\n",temp.a,temp.b);
//system("pause");
//printf("%I64d\n",gcd(temp.a,temp.b));
if(temp.a)
{
ll te=gcd(temp.a,temp.b);
temp.a/=te;
temp.b/=te;
}
else
temp.b=0;
B[i]=temp;
//printf("i:%d %I64d %I64d\n",i,B[i].a,B[i].b);
//system("pause");
}
}
int main()
{
//freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
//printf("%I64d\n",gcd(-6,12));
init();
while(~scanf("%I64d",&k))
{
ll cur=1;
for(int i=0;i<=k;i++)
{
if(i==1)
{
ans[i].a=k+1; //B[1]=-1/2要加上后面多出来的n^k
ans[i].b=2;
}
else
{
ans[i]=B[i];
ans[i].a*=C[k+1][i];
}
if(ans[i].a) //约分
{
ll temp=gcd(ans[i].a,ans[i].b);
ans[i].a/=temp;
ans[i].b/=temp;
}
else
ans[i].b=0;
if(ans[i].b) //求分母的最小公倍数
cur=cur/gcd(cur,ans[i].b)*ans[i].b;
}
printf("%I64d ",cur*(k+1));
//printf("->%I64d %I64d %I64d\n",cur,ans[0].a,ans[0].b);
for(int i=0;i<=k;i++) //求出通分后每一个系数
{
if(ans[i].b)
ans[i].a=cur/ans[i].b*ans[i].a;
//printf("i:%d %I64d\n",i,ans[i].a);
}
for(int i=0;i<=k;i++)
printf("%I64d ",ans[i].a);
printf("0\n"); //最后一个肯定是0
}
return 0;
}
[伯努利数] poj 1707 Sum of powers,布布扣,bubuko.com
原文:http://blog.csdn.net/cc_again/article/details/24764911