很水两题,C题数论果然不太会,事后4题。。
The bear decided to store some raspberry for the winter. He cunningly found out the price for a barrel of honey in kilos of raspberry for each of the following n days.
According to the bear‘s data, on the i-th (1?≤?i?≤?n) day,
the price for one barrel of honey is going to is xikilos
of raspberry.
Unfortunately, the bear has neither a honey barrel, nor the raspberry. At the same time, the bear‘s got a friend who is ready to lend him a barrel of honey for exactly one day for c kilograms
of raspberry. That‘s why the bear came up with a smart plan. He wants to choose some day d (1?≤?d?<?n),
lent a barrel of honey and immediately (on day d) sell it according to a daily exchange rate. The next day (d?+?1) the
bear wants to buy a new barrel of honey according to a daily exchange rate (as he‘s got some raspberry left from selling the previous barrel) and immediately (on day d?+?1)
give his friend the borrowed barrel of honey as well as c kilograms of raspberry for renting the barrel.
The bear wants to execute his plan at most once and then hibernate. What maximum number of kilograms of raspberry can he earn? Note that if at some point of the plan the bear runs out of the raspberry, then he won‘t execute such a plan.
Output
Print a single integer — the answer to the problem.
Note
In the first sample the bear will lend a honey barrel at day 3 and then sell it for 7. Then the bear will buy a barrel for 3 and return it to the friend. So, the profit is (7 - 3 - 1) = 3.
In the second sample bear will lend a honey barrel at day 1 and then sell it for 100. Then the bear buy the barrel for 1 at the day 2. So, the profit is (100 - 1 - 2) = 97.
A题:水题,要注意点 小于0的答案输出0.
代码:
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
int n, c, num[105], i;
int main() {
int ans = 0;
scanf("%d%d", &n, &c);
for (i = 0; i < n; i++)
scanf("%d", &num[i]);
for (i = 0; i < n - 1; i++)
if (num[i] - num[i + 1] > ans)
ans = num[i] - num[i + 1];
if (ans - c < 0) printf("0\n");
else printf("%d\n", ans - c);
return 0;
}
The bear has a string s?=?s1s2... s|s| (record |s| is
the string‘s length), consisting of lowercase English letters. The bear wants to count the number of such pairs of indices i,?j (1?≤?i?≤?j?≤?|s|),
that string x(i,?j)?=?sisi?+?1... sj contains
at least one string "bear" as a substring.
String x(i,?j) contains string "bear",
if there is such index k (i?≤?k?≤?j?-?3),
that sk?=?b, sk?+?1?=?e, sk?+?2?=?a, sk?+?3?=?r.
Help the bear cope with the given problem.
Output
Print a single number — the answer to the problem.
Note
In the first sample, the following pairs (i,?j) match: (1,?4),?(1,?5),?(1,?6),?(1,?7),?(1,?8),?(1,?9).
In the second sample, the following pairs (i,?j) match: (1,??4),?(1,??5),?(1,??6),?(1,??7),?(1,??8),?(1,??9),?(1,??10),?(1,??11),?(2,??10),?(2,??11),?(3,??10),?(3,??11),?(4,??10),?(4,??11),?(5,??10),?(5,??11),?(6,??10),?(6,??11),?(7,??10),?(7,??11).
B题:问有几个包含至少一个bear字串。
思路:O(n)。每次找到bear就计算前面字母个数x和后面字母个数y,然后(x + 1) * (y + 1) - 上一个的(x + 1) * (y + 1)(用来除去重复的)
代码:
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
char str[5005];
__int64 i, j, x, y;
__int64 ans = 0;
int main() {
scanf("%s", str);
__int64 len = strlen(str);
x = 0;
for (i = 0; i < len - 3; i++) {
if (str[i] == ‘b‘ && str[i + 1] == ‘e‘ && str[i + 2] == ‘a‘ && str[i + 3] == ‘r‘) {
ans += (i + 1) * (len - i - 3) - (len - i - 3) * x;
x = i + 1;
}
}
printf("%I64d\n", ans);
return 0;
}
Recently, the bear started studying data structures and faced the following problem.
You are given a sequence of integers x1,?x2,?...,?xn of
length n and m queries, each of them is characterized
by two integers li,?ri.
Let‘s introduce f(p) to represent the number of such indexes k,
that xk is divisible
by p. The answer to the query li,?ri is
the sum: 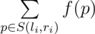 ,
where S(li,?ri) is
a set of prime numbers from segment [li,?ri] (both
borders are included in the segment).
,
where S(li,?ri) is
a set of prime numbers from segment [li,?ri] (both
borders are included in the segment).
Help the bear cope with the problem.
Output
Print m integers — the answers to the queries on the order the queries appear in the input.
Note
Consider the first sample. Overall, the first sample has 3 queries.
-
The first query l?=?2, r?=?11 comes. You need to
count f(2)?+?f(3)?+?f(5)?+?f(7)?+?f(11)?=?2?+?1?+?4?+?2?+?0?=?9.
-
The second query comes l?=?3, r?=?12. You need to
count f(3)?+?f(5)?+?f(7)?+?f(11)?=?1?+?4?+?2?+?0?=?7.
-
The third query comes l?=?4, r?=?4. As this interval
has no prime numbers, then the sum equals 0.
C题:直接在筛素数的过程把和求出来即可,然后用前缀和访问每个区间的和
代码:
#include <stdio.h>
#include <string.h>
const int N = 10000001;
int vis[N], sum[N], v[N];
void init() {
int num, n;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &num);
vis[num]++;
}
}
void cal() {
for (int i = 2; i < N; i++) {
if (v[i]) continue;
for (int j = i; j < N; j += i) {
if (vis[j]) sum[i] += vis[j];
v[j] = 1;
}
}
}
void solve() {
for (int i = 2; i < N; i++)
sum[i] += sum[i - 1];
int m, l, r;
scanf("%d", &m);
while (m--) {
scanf("%d%d", &l, &r);
if (r >= N) r = N - 1;
if (l >= N) l = N;
printf("%d\n", sum[r] - sum[l - 1]);
}
}
int main() {
init();
cal();
solve();
return 0;
}
One day a bear lived on the Oxy axis. He was afraid of the dark, so he couldn‘t move at night along the plane points that aren‘t lit. One day the bear wanted
to have a night walk from his house at point (l,?0) to his friend‘s house at point (r,?0),
along the segment of length(r?-?l). Of course, if he wants to make this walk, he needs each point of the segment to be lit. That‘s why the bear
called his friend (and yes, in the middle of the night) asking for a very delicate favor.
The Oxy axis contains n floodlights. Floodlight i is
at point (xi,?yi) and
can light any angle of the plane as large as ai degree
with vertex at point (xi,?yi).
The bear asked his friend to turn the floodlights so that he (the bear) could go as far away from his house as possible during the walking along the segment. His kind friend agreed to fulfill his request. And while he is at it, the bear wonders: what is the
furthest he can go away from his house? Hep him and find this distance.
Consider that the plane has no obstacles and no other light sources besides the floodlights. The bear‘s friend cannot turn the floodlights during the bear‘s walk. Assume that after all the floodlights are turned in the correct direction, the bear goes for a
walk and his friend goes to bed.
Output
Print a single real number — the answer to the problem. The answer will be considered correct if its relative or absolute error doesn‘t exceed 10?-?6.
思路:dp+几何,在计算灯能覆盖的面积的时候,利用向量的方法去求,然后dp求最大长度。
代码:
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
using namespace std;
#define min(a,b) ((a)<(b)?(a):(b))
#define max(a,b) ((a)>(b)?(a):(b))
const int N = 25;
const double pi = acos(-1.0);
int n;
double l, r, dp[1<<20];
struct D {
double x, y, du;
void scan() {
scanf("%lf%lf%lf", &x, &y, &du);
du = du * pi / 180.0;
x -= l;
}
} d[N];
double cal(int i, double x0) {
double dx = x0 - d[i].x;
double dy = -d[i].y;
double x1 = dx * cos(d[i].du) - dy * sin(d[i].du);
double y1 = dx * sin(d[i].du) + dy * cos(d[i].du);
if (fabs(y1) < 1e-12 || y1 > 0) return r;
return min(r, d[i].x - d[i].y * x1 / y1);
}
void init() {
scanf("%d%lf%lf", &n, &l, &r); r -= l;
for (int i = 0; i < n; i++)
d[i].scan();
}
double solve() {
for (int i = 0; i < (1<<n); i++) {
for (int j = 0; j < n; j++) {
if (i&(1<<j)) continue;
dp[i|(1<<j)] = max(dp[i|(1<<j)], cal(j, dp[i]));
}
}
return dp[(1<<n) - 1];
}
int main() {
init();
printf("%.9lf\n", solve());
return 0;
}
E题:应该是矩阵快速幂,暂时没什么想法。都以后有想法回头补上
UML图(一) 综述
原文:http://blog.csdn.net/u010191243/article/details/18714585

 ,
where
,
where