POJ 2676 数码问题DLX

Description

Sudoku is a very simple task. A square table with 9 rows and 9 columns is divided to 9 smaller squares 3x3 as shown on the Figure. In some of the cells are written decimal digits from 1 to 9. The other cells are empty. The goal is to fill the empty cells with decimal digits from 1 to 9, one digit per cell, in such way that in each row, in each column and in each marked 3x3 subsquare, all the digits from 1 to 9 to appear. Write a program to solve a given Sudoku-task.

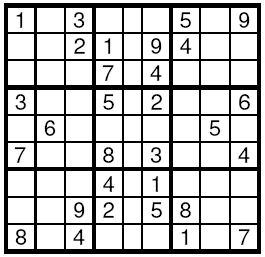
Input

Output

Sample Input

1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107

Sample Output

143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127

与POJ 3076一样的方法。

代码：

/* ***********************************************
Author :_rabbit
Created Time :2014/5/1 8:56:15
File Name :F.cpp
************************************************ */
#pragma comment(linker, "/STACK:102400000,102400000")
#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <sstream>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#include <string>
#include <time.h>
#include <math.h>
#include <queue>
#include <stack>
#include <set>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define eps 1e-8
#define pi acos(-1.0)
typedef long long ll;
struct DLX{
    const static int maxn=20010;
    #define FF(i,A,s) for(int i = A[s];i != s;i = A[i])
    int L[maxn],R[maxn],U[maxn],D[maxn];
    int size,col[maxn],row[maxn],s[maxn],H[maxn];
    bool vis[70];
	int ans[maxn],cnt;
    void init(int m){
        for(int i=0;i<=m;i++){
            L[i]=i-1;R[i]=i+1;U[i]=D[i]=i;s[i]=0;
        }
        memset(H,-1,sizeof(H));
        L[0]=m;R[m]=0;size=m+1;
    }
	void link(int r,int c){
         U[size]=c;D[size]=D[c];U[D[c]]=size;D[c]=size;
         if(H[r]<0)H[r]=L[size]=R[size]=size;
         else {
             L[size]=H[r];R[size]=R[H[r]];
             L[R[H[r]]]=size;R[H[r]]=size;
         }
         s[c]++;col[size]=c;row[size]=r;size++;
     }
	void del(int c){//精确覆盖
        L[R[c]]=L[c];R[L[c]]=R[c];  
        FF(i,D,c)FF(j,R,i)U[D[j]]=U[j],D[U[j]]=D[j],--s[col[j]];  
    }  
    void add(int c){  //精确覆盖
        R[L[c]]=L[R[c]]=c;  
        FF(i,U,c)FF(j,L,i)++s[col[U[D[j]]=D[U[j]]=j]];  
    }  
	bool dfs(int k){//精确覆盖
        if(!R[0]){  
            cnt=k;return 1;  
        }  
        int c=R[0];FF(i,R,0)if(s[c]>s[i])c=i;  
        del(c);  
        FF(i,D,c){  
            FF(j,R,i)del(col[j]);  
            ans[k]=row[i];if(dfs(k+1))return true;  
            FF(j,L,i)add(col[j]);  
        }  
        add(c);  
        return 0;
    }  
    void remove(int c){//重复覆盖
        FF(i,D,c)L[R[i]]=L[i],R[L[i]]=R[i];
    }
     void resume(int c){//重复覆盖
         FF(i,U,c)L[R[i]]=R[L[i]]=i;
     }
    int A(){//估价函数
        int res=0;
        memset(vis,0,sizeof(vis));
        FF(i,R,0)if(!vis[i]){
                res++;vis[i]=1;
                FF(j,D,i)FF(k,R,j)vis[col[k]]=1;
            }
        return res;
    }
    void dfs(int now,int &ans){//重复覆盖
        if(R[0]==0)ans=min(ans,now);
        else if(now+A()<ans){
            int temp=INF,c;
            FF(i,R,0)if(temp>s[i])temp=s[i],c=i;
            FF(i,D,c){
                remove(i);FF(j,R,i)remove(j);
                dfs(now+1,ans);
                FF(j,L,i)resume(j);resume(i);
            }
        }
    }
}dlx;
const int SLOT=0;
const int ROW=1;
const int COL=2;
const int SUB=3;
int encode(int a,int b,int c){
	return a*81+b*9+c+1;
}
void decode(int code,int &a,int &b,int &c){
	code--;
	c=code%9;code/=9;
	b=code%9;code/=9;
	a=code;
}
char str[20][20];
int main()
{
     //freopen("data.in","r",stdin);
     //freopen("data.out","w",stdout);
     int T;
	 cin>>T;
	 while(T--){
		 for(int i=0;i<9;i++)scanf("%s",str[i]);
		 dlx.init(324);
		 for(int r=0;r<9;r++)
			 for(int c=0;c<9;c++)
				 for(int k=1;k<=9;k++)
					 if(str[r][c]==‘0‘||str[r][c]==k+‘0‘){
						 int p=encode(r,c,k-1);
						 dlx.link(p,encode(SLOT,r,c));
						 dlx.link(p,encode(ROW,r,k-1));
						 dlx.link(p,encode(COL,c,k-1));
						 dlx.link(p,encode(SUB,(r/3)*3+c/3,k-1));
					 }
		 dlx.dfs(0);
		// cout<<"jjjdfjfj"<<endl;
		//cout<<"hhahha: "<<dlx.cnt<<endl;
		 for(int i=0;i<dlx.cnt;i++){
			 int r,c,v;
			 decode(dlx.ans[i],r,c,v);
			// cout<<"pppp"<<endl;
			// cout<<"han "<<r<<" "<<c<<" "<<v<<endl;
			 str[r][c]=v+‘1‘;
		 }
		 for(int i=0;i<9;i++)printf("%s\n",str[i]);
	 }
     return 0;
}

POJ 2676 数码问题DLX,布布扣,bubuko.com

POJ 2676 数码问题DLX

原文：http://blog.csdn.net/xianxingwuguan1/article/details/24835221