一.简述
利用链表表示稀疏多项式,并基于之前的一些操作(编程实现上还是有所不同的)组合新的操作实现一元多项式的表示及相加。
二.ADT

1 抽象数据类型一元多项式的定义 2 ADT Polyomail{ 3 数据对象:D = {a[i]|a[i]属于TermSet, i = 1,2,3...,m,m>=0 4 TermSet中每个元素包含一个表示系数的实数和表示指数的整数} 5 数据关系 6 基本操作: 7 CreatPolyn(&P, m) 8 操作结果:输入 m 项的系数和指数,建立一元多项式 P 9 DestroyPolyn(&P) 10 初始条件:一元多项式 P 已存在 11 操作结果:销毁一元多项式P 12 PrintPolyn(P) 13 初始条件:一元多项式 P 已存在 14 操作结果:打印输出一元多项式 P 15 PolynLength(P) 16 初始条件:一元多项式 P 已存在 17 操作结果:返回一元多项式中 P 的项数 18 AddPolyn(&Pa, &Pb) 19 初始条件:一元多项式 Pa 和 Pb 已存在 20 操作结果:完成多项式相加运算,即:Pa = Pa + Pb,并销毁一元多项式 Pb 21 SubtractPolyn(&Pa, &Pb) 22 初始条件:一元多项式 Pa 和 Pb 已存在 23 操作结果:完成多项式相减运算,即 Pa = Pa - Pb,并销毁一元多项式 Pb 24 MultiplyPolyn(&Pa, &Pb) 25 初始条件:一元多项式 Pa 和 Pb 已存在 26 操作结果:完成多项式相乘运算,即 Pa = Pa x Pb,并销毁一元多项式 Pb 27 }ADT Polynomial 28 */
三.头文件

1 //2_4.h 2 /** 3 《数据结构(C语言版)》 Page 37 4 ....为此,从实际应用角度出发重新定义线性链表及其基本操作.... 5 */ 6 /** 7 author:zhaoyu 8 email:zhaoyu1995.com@gmail.com 9 date:2016-6-6 10 note:realize my textbook <<数据结构(C语言版)>> 11 */ 12 #ifndef _2_4_H_ 13 #define _2_4_H_ 14 #include "head.h" 15 typedef struct{//项的表示,多项式的项作为LinkList的数据元素 16 float coef;//系数 17 int expn;//指数 18 }term, ElemType;//两个类型名:term用于本ADT,ElemType为LinkList的数据对象名 19 typedef struct LNode{ 20 ElemType data; 21 struct LNode *next; 22 }*Link, *Position; 23 typedef struct{//链表类型 24 Link head, tail;//分别指向线性链表中的头结点和最后一个结点 25 int len;//指示线性链表中数据元素的个数 26 }LinkList; 27 typedef LinkList polynomial;//用带表头结点的有序链表表示多项式 28 29 int cmp(term a, term b) 30 { 31 //依据 a 的指数值 <(或=)(或>) b 的指数值 ,返回 -1 ,0, +1 32 if(a.expn < b.expn) 33 { 34 return -1; 35 } 36 else if (a.expn == b.expn) 37 { 38 return 0; 39 } 40 else 41 { 42 return 1; 43 } 44 } 45 Status InitList(LinkList &L) 46 { 47 //构造一个空的线性表L 48 L.head = (Link)malloc(sizeof(struct LNode)); 49 L.head->data.coef = 0.0; 50 L.head->data.expn = -1; 51 L.head->next = NULL; 52 L.tail = L.head->next; 53 L.len = 0; 54 } 55 Position GetHead(LinkList L) 56 { 57 //返回线性链表 L 中头结点的位置 58 return L.head; 59 } 60 Status SetCurElem(Link &p, ElemType e) 61 { 62 //已知 p 指向线性链表中的一个结点,用 e 更新 p 所指结点中数据元素的值 63 p->data.coef = e.coef; 64 p->data.expn = e.expn; 65 return OK; 66 } 67 Status LocateElem(LinkList L, ElemType e, Position &q, Status (* compare)(ElemType, ElemType)) 68 { 69 //若有序链表 L 中存在与 e 满足判定函数 compare() 取值为 0 的函数 70 //则 q 指示 L 中第一个值为 e 的结点的位置,并返回 TRUE;否则 q 指示 71 //第一个与 e 满足compare() 取值>0的元素的前驱的位置,并返回FLASE 72 Link temp = L.head->next; 73 while (temp != NULL) 74 { 75 if (0 == (* compare)(temp->data, e)) 76 { 77 q = temp; 78 return TRUE; 79 } 80 temp = temp->next; 81 } 82 temp = L.head; 83 while (temp->next != NULL) 84 { 85 if ((* compare)(temp->next->data, e) > 0) 86 { 87 q = temp; 88 return FALSE; 89 } 90 temp = temp->next; 91 } 92 q = temp; 93 return FALSE; 94 } 95 Status MakeNode(Link &p, ElemType e) 96 { 97 //分配由 p 指向的值为 e 的结点,并返回 OK;若分配失败,则返回 ERROR 98 p = (Link)malloc(sizeof(struct LNode)); 99 if (!p) 100 { 101 return ERROR; 102 } 103 p->data.coef = e.coef; 104 p->data.expn = e.expn; 105 p->next = NULL; 106 return OK; 107 } 108 Status InsFirst(Link &h, Link &s) 109 { 110 //已知 h 指向线性链表的头结点,将 s 所指节点插入在第一个结点之前 111 if (NULL == h) 112 { 113 return ERROR; 114 } 115 else 116 { 117 s->next = h->next; 118 h->next = s; 119 } 120 return OK; 121 } 122 ElemType GetCurElem(Link p) 123 { 124 //已知 p 指向线性链表中的一个节点,返回 p 所指结点中数据元素的值 125 if (p != NULL) 126 { 127 return p->data; 128 } 129 else 130 { 131 exit(ERROR); 132 } 133 } 134 /** 135 My Code 136 */ 137 Position NextPos(LinkList L, Link p) 138 { 139 //已知 p 指向线性链表 L 中的一个节点,返回 p 所指结点 140 //的直接后继的位置,若无后继,返回 NULL 141 Link q = L.head; 142 while (q->next != NULL) 143 { 144 if(q == p) 145 { 146 return p->next; 147 } 148 q = q->next; 149 } 150 return NULL; 151 } 152 Status DelFirst(Link &h, Link &q) 153 { 154 //已知 h 指向线性链表的头结点,删除链表中的第一个节点并以 q 返回 155 if (h == NULL) 156 { 157 return ERROR; 158 } 159 q = h->next; 160 h->next = q->next; 161 q->next = NULL; 162 return OK; 163 } 164 Status FreeNode(Link &p) 165 { 166 //释放 p 所指节点 167 p = NULL;//便于回收???释放后再次使用 168 free(p); 169 } 170 Status ListEmpty(LinkList L) 171 { 172 //若线性链表 L 为空,则返回 TRUE,否则返回 FALSE 173 if (L.head->next == NULL) 174 { 175 return TRUE; 176 } 177 else 178 { 179 return FALSE; 180 } 181 } 182 Status Append(LinkList &L, Link &s) 183 { 184 //将指针 s 所指(彼此以指针相链)的一串结点 185 //链接在线性链表 L 最后一个结点 186 Link q = L.head; 187 while (q->next != NULL) 188 { 189 q = q->next; 190 } 191 q->next = s; 192 int cnt = 0; 193 Link temp = s; 194 while (temp != NULL) 195 { 196 cnt++; 197 if (NULL == temp->next) 198 { 199 L.tail = temp;//注意更新尾指针 200 } 201 temp = temp->next;//注意这一句要放在最后,否则可能访问非法内存 202 } 203 204 L.len += cnt; 205 //注意要根据这一串结点长度增加链表长度 206 return OK; 207 } 208 void PrintPolyn(polynomial P) 209 { 210 Link temp = P.head->next; 211 while (temp != NULL) 212 { 213 printf("%.1f\t", temp->data.coef); 214 temp = temp->next; 215 } 216 printf("\n"); 217 temp = P.head->next; 218 while (temp != NULL) 219 { 220 printf("%d\t", temp->data.expn); 221 temp = temp->next; 222 } 223 printf("\n"); 224 } 225 /** 226 algorithm 2.22 227 */ 228 void CreatPolyn(polynomial &P, int m) 229 { 230 //输入 m 项的系数和指数,建立表示一元多项式的有序链表 P 231 InitList(P); 232 Link h = GetHead(P), s, q; 233 ElemType e; 234 e.coef = 0.0; 235 e.expn = -1; 236 SetCurElem(h, e);//设置头结点中的数据元素 237 for (int i = 1; i <= m; i++) 238 {//依次输入 m 个非零项 239 scanf("%f%d", &e.coef, &e.expn); 240 if (!LocateElem(P, e, q, (* cmp))) 241 {//当前链表中不存在该指数项 242 if (MakeNode(s, e)) 243 { 244 InsFirst(q, s); 245 } 246 } 247 } 248 }//CreatePolyn 249 /** 250 algorithm 2.23 251 */ 252 void AddPolyn(polynomial &Pa, polynomial &Pb) 253 { 254 //多项式加法:Pa = Pa + Pb,利用两个多项式构成和多项式 255 Link ha = GetHead(Pa); 256 Link hb = GetHead(Pb);//pa 和 pb 分别指向 Pa 和 Pb 的头结点 257 Link qa = NextPos(Pa, ha); 258 Link qb = NextPos(Pb, hb);//qa 和 qb 分别指向 Pa 和 Pb 中当前节点 259 while (qa && qb)//qa 和 qb均非空 260 { 261 ElemType a = GetCurElem(qa); 262 ElemType b = GetCurElem(qb);//a、b为两表中当前比较元素 263 switch ((* cmp)(a, b)) 264 { 265 case -1://多项式 Pa 中当前节点的指数值小 266 { 267 ha = qa; 268 qa = NextPos(Pa, qa);//printf("%d\n", qa->data.expn); 269 break; 270 } 271 case 0://两者的指数值相等 272 { 273 ElemType S = {a.coef + b.coef, a.expn}; 274 if(0 != S.coef) 275 {//修改多项式 Pa 中当前节点 276 SetCurElem(qa, S); 277 ha = qa; 278 } 279 else 280 {//删除多项式中 Pa 当前节点 281 DelFirst(ha, qa); 282 FreeNode(qa); 283 } 284 DelFirst(hb, qb); 285 FreeNode(qb); 286 qa = NextPos(Pa, ha); 287 qb = NextPos(Pb, hb); 288 break; 289 } 290 case 1://多项式 Pb 当前结点指数值小 291 { 292 DelFirst(hb, qb); 293 InsFirst(ha, qb); 294 qb = NextPos(Pb, hb); 295 ha = NextPos(Pa, ha); 296 break; 297 } 298 }//switch 299 }//while 300 if (!ListEmpty(Pb)) 301 { 302 Append(Pa, qb);//链接 Pb 中剩余结点 303 } 304 FreeNode(hb);//释放 Pb 的头结点 305 }//AddPolyn 306 #endif
四.CPP文件

1 #include "2_4.h" 2 3 int main(int argc, char const *argv[]) 4 { 5 polynomial Pa, Pb, Pc; 6 int n; 7 printf("Input n\t"); 8 scanf("%d", &n); 9 CreatPolyn(Pa, n); 10 printf("Pa\n"); 11 PrintPolyn(Pa); 12 printf("Input n\t"); 13 scanf("%d", &n); 14 CreatPolyn(Pb, n); 15 printf("Lb\n"); 16 PrintPolyn(Pb); 17 AddPolyn(Pa, Pb); 18 printf("La + Lb\n"); 19 PrintPolyn(Pa); 20 return 0; 21 }
五.测试
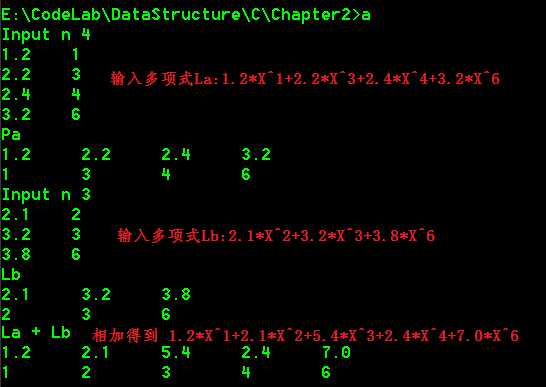
六.小结
不要对着伪代码一行行敲代码,一定要在理解的基础上实现算法,否则敲错一个变量导致奇怪的错误也要大费周折才能找到。
数据结构算法C语言实现(六)---2.4一元多项式的表示及相加
原文:http://www.cnblogs.com/zhaoyu1995/p/5567137.html