Uva:11401
数三角形:有多少种方法可以从1,2,3,…,n中选出3个不同的整数,使得以它们为三边长可以组成三角形?(n≤1000000)
分析:如果直接暴力,参考n的取值范围,O(n^3)的复杂度势必不堪重负,因此这里需要一定的数学推导。
我们设c(x)为最大边长为x的三角形个数,f(n)为题目的解,则有f(n) = ∑c(i),转化成递推式,有f(n) = f(n-1) + c(n).
下面我们需要讨论如何计算c(n):设三角形三边为x、y、z,x是最大边,则有y + z > x,则对于y将满足不等式x-z<y<x,现在另z遍历[1,x-1].
z = 1,y无解;
z = 2,y=x-1;
z = 3,y=x-1或y=x-2;
…
容易找到规律,对于z取得整数i,对应y有i-1组解,那么看似c(x) = 0 + 1 + 2 +…+x-2 = (x-1)(x-2)/2.
但是我们注意到这个模式中y、z的对称性,即二元组(y,z)是无序的,但是这里我们显然将其当成有序的来处理,这表明这种方法每个三角形我们计算了两次。
还有一个问题,我们的这种计算模式包含了y = z的情况,因此我们应该想办法去掉。
当z=i,y能够取得的最小值是x-i+1,当x-i+1≤i的时候,出现y=z的情况,即x-1≥i≥(x+1)/2。即有x -1 – (x+1)/2 + 1 = x – (x+1)/2 = (x-1)/2,由于(x+1)/2是向上取整的,则(x-1)/2应该是向下取整。考虑到c(x)表达的实际意义,c(x)本身也应该向下取整。
综上,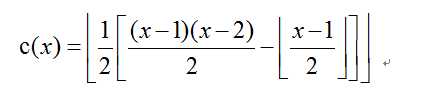
简单的参考代码如下:
#include<iostream> using namespace std; long long f[1000000 + 5]; int main() { f[3] = 0; for(long long x = 4;x <= 1000000;x++) f[x] = f[x-1] + ((x-1)*(x-2)/2 - (x-1)/2)/2; long long n; while(cin >> n) { if(n < 3) break; else cout<<f[n]<<endl; } return 0; }
Uva:11806
在一个m行n列的矩形网格里放k个相同的石子,问有多少种方法?每个格子最多放一个石子,所有石子都要用完,并且第一行、最后一行、第一列、最后一列都得有石子。
分析:这里我们利用组合公式C(rc,k)容易直接给出的是在r行c列中放入k个石子的方案数,但是这里加上四个限制条件,我们应该思考的就是做出一些巧妙的等价转化。
考虑到数学当中常用到的逆向思维,原题的限制是第一行且最后一行且第一列且最后一列都得有石子,那么其反面则为第一行没石子或最后一行没石子或第一列没石子或最后一列没石子,那么现在我们想要求这个反面,简单的模拟一下,对于第一行没石子,我们容易得到C((m-1)n,k),对于第一列没石子,我们容易得到C((n-1)m,k)种情况,那么问题来了,那些第一列没有石子、第一行也没有石子的情况,就没重复记入了两次,对于其余的情况也存在类此的重复,因此这里我们考虑应用容斥定理。
四个条件分别为A、B、C、D(表示不放入石子),我们利用二级制数来表示来表示出16种搭配方式,设最终解为f(m,n,k),则有如下的计算公式。
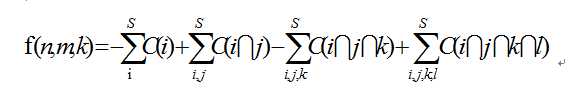
其中S = {A,B,C,D}.
参考代码如下。
#include<iostream> #include<cstring> #include<cstdio> using namespace std; const int mod = 1000007; const int maxn = 450; int main() { int C[maxn][maxn]; memset(C, 0 ,sizeof(C)); for(int i = 0; i < maxn;i++) { C[i][0] = C[i][i] = 1; for(int j = 1;j < maxn;j++) C[i][j] = (C[i-1][j-1] + C[i-1][j])%mod; } // printf("%d",C[15][14]); int t; scanf("%d",&t); int iCase = 1; while(t--) { int sum = 0; int n , m , k; scanf("%d%d%d",&n,&m,&k); for(int i = 0;i < 16;i++) { int r = n , c = m , b = 0; //初始化的位置一定要搞清楚,要放在for循环里面,因为16种情况每次开始的时候都应该初始化一遍 if(i & 1) {b++;c--;} if(i & 2) {b++;c--;} if(i & 4) {b++;r--;} if(i & 8) {b++;r--;} if(b&1) {sum = (sum + mod -C[r*c][k]) % mod;} else {sum = (sum + C[r*c][k]) % mod;} } printf("Case %d: %d\n",iCase++ , sum); } }
递推关系:
卡特兰数:对于n凸多边形,用n-3条不相交的对角线将多边形划分长成n-2个三角形,有多少种划分方法?
分析:设C[n]为该题结果,我们从某点开始对凸多边形的顶点顺时针进行标号,从v1到vn。我们以边<v1,vn>为基边,最终的剖分结果中,<v1,vn,vk>必然形成一个三角形,而此时n凸多边形被进一步划分成k+1边形和n-1-k边形,则得到C[k+1]C[n-1-k]种情况,遍历k便可以得到所有情况。即有如下递推公式成立:
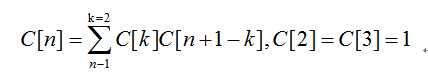
原文:http://www.cnblogs.com/rhythmic/p/5571942.html